Question

If $(2i + 6i + 27k) \times (i + \lambda j + \mu k) = 0$ then $\lambda$ and $\mu$ are respectively.

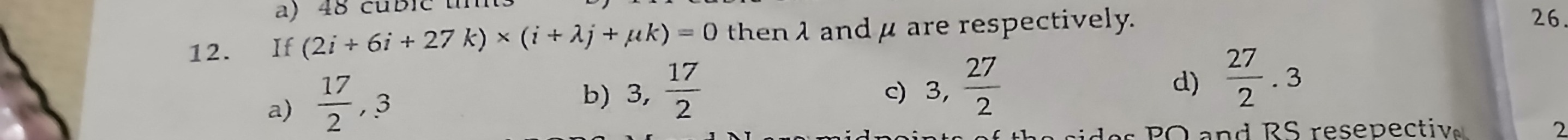
• A. $\frac{17}{2}, 3$
• B. $3, \frac{17}{2}$
• C. $3, \frac{27}{2}$
• D. $\frac{27}{2}, 3$

Answer 1

Answer: (C)

$\lambda = 3$ and $\mu = \frac{27}{2}$

Answer 2

Vectors $\vec{A}$ and $\vec{B}$ are collinear as their cross product is zero.
Equate $\vec{B}=k\vec{A}$.
From the $i$-component, $k=\frac{1}{2}$.
Thus, $\lambda=3$ and $\mu=\frac{27}{2}$.