Question

A 44 mH inductor is connected to 220 V, 50 Hz ac supply. Determine the rms value of the current in the circuit.

Answer 1

Hint: To solve this question we should use the ac through the inductor concept. Obtain the expression for reactance and find its value by putting the given value. Then with the help of the relation between the current, voltage and reactance we can get the value of current.

Complete step by step answer:
An inductor can be defined as a two terminal passive electrical component which can store energy in a magnetic field when current is flowing through it.

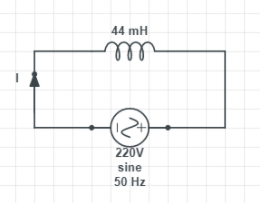
In the question we are given that the inductor has an inductance of, $L=44mH$
The voltage of the power supply is $V=220V$ and the frequency of power supply is $\nu =50Hz$.
We have a quantity called reactance which can be defined as the ratio of the peak voltage to the peak current in the inductor due to an AC power supply. It is given the mathematical expression,
$\begin{aligned} & {{X}_{L}}=\dfrac{{{V}_{P}}}{{{I}_{P}}}=\dfrac{\omega L{{I}_{P}}}{{{I}_{P}}} \\\ & {{X}_{L}}=\omega L \\\ \end{aligned}$
Where, $\omega$ is the angular frequency which can be written as, $\omega =2\pi \nu$ , where $\nu$ is the linear frequency.
So, we can write the above equation as,
${{X}_{L}}=2\pi \nu L$
Putting the given values, we get,
$\begin{aligned} & {{X}_{L}}=2\pi \times 50Hz\times 44\times {{10}^{-3}}H \\\ & {{X}_{L}}=13.816\Omega \\\ \end{aligned}$
Now, we have the relation between the reactance and the current in the circuit as,
$I=\dfrac{{{V}_{rms}}}{{{X}_{L}}}$
Again, putting the given values, we get,
$\begin{aligned} & I=\dfrac{220V}{13.816\Omega } \\\ & I=15.9A \\\ \end{aligned}$
So, current through the circuit is 15.9A

Note: With some other quantities the value of inductance is also given by the equation,
$L=\dfrac{{{V}_{L}}}{\left( \dfrac{di}{dt} \right)}$, where l is the inductance, ${{V}_{L}}$ is the voltage across the coil and $\dfrac{di}{dt}$ is the rate of change of current.
Unit of inductance is Henry. It can be defined as the inductance of a coil when the change in the coil with a voltage of 1V across it is one ampere per second.