Question

A $40kg$ slab rests on a frictionless floor as shown in the figure. A $10kg$ block rests on top of the slab. The static coefficient of friction between the block and the slab is 0.60 while the kinetic coefficient is 0.40. The $10kg$ block is acted upon by a horizontal force of 100N. If $g = 10m/{s^2}$ the resulting acceleration of the slab will be?

Answer 1

Analyse whether the blocks move together or not, and for that find acceleration of total mass and then use the appropriate formula to find the acceleration and then solve it further to get the Answer.

Complete step by step answer:

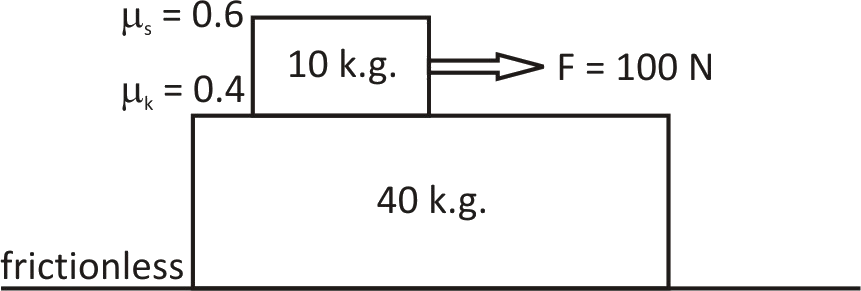
Here it is given that
A 40kg slab rests on a frictionless floor and a 10kg block rests on top of the slab
The value of static coefficient of friction in between the given slab and block is${\mu _s} = 0.60$
The value of kinetic coefficient of friction in between the given slab and block is${\mu _k} = 0.40$
As per given-
1. Maximum Static Friction Force-
${({F_{rs}})_{\max }} = {\mu _s} \times R$ [R=Reaction Force, R=mg]
Now, Putting the values in the formula we have
${({F_{rs}})_{\max }} = 0.6 \times 10 \times 10 = 60N$
2. Kinetic Friction Force-
$({F_{rk}}) = {\mu _k} \times R = 0.4 \times 10 \times 10 = 40N$

Now,
Case 1: If both the block and slab move together

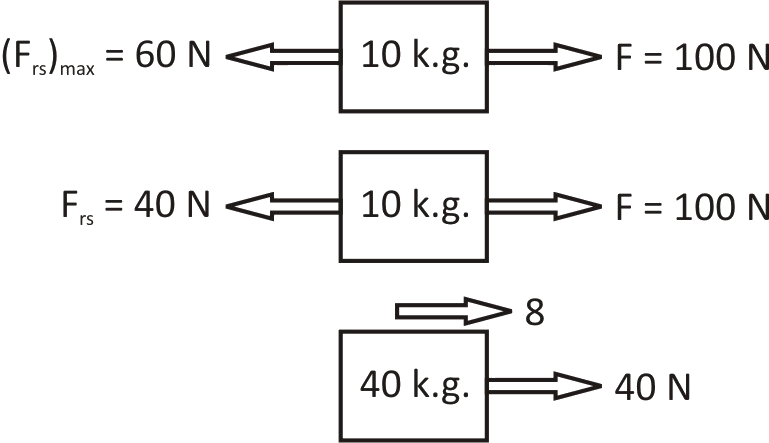
This is not possible because $F > ({F_{rs}})\max$
Case 2- Relative Motion between block and slab

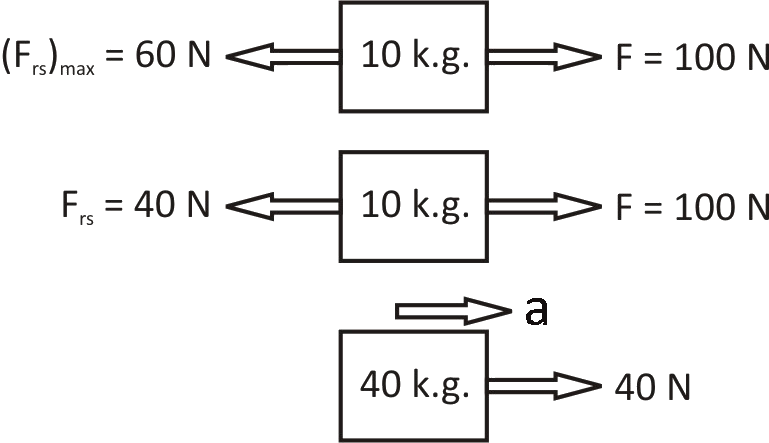
In this case according to the free body diagram as shown above: For 40 kg slab the net force will be :
${F_{net}} = 40N$

$$\Rightarrow m \times a = 40N \\\ \Rightarrow F = {\mu _m}^1g \\\ \Rightarrow a = \dfrac{f}{m} \\\$$

$a = \dfrac{{40}}{{40}} = 1m/{s^2}$

Note:
Whenever such types of question appears then always write down the things given in the question then find the acceleration of total mass due to the application of a horizontal force of 100N on the block of 10kg and then find the maximum frictional force on the block, then we observe that the frictional force is smaller than the applied force and it proves that the block and the slab are not moving relative to each other. So, we can write for the block that${\text{F = }}{{\text{\mu }}_{\text{m}}}^{\text{1}}{\text{g}}$ and then after finding the value of F.