Solveeit Logo
Login

Question

Question: A \(4000Kg\) truck is parked on a \({{7.0}^{\circ }}\) slope. How big is the friction force on the t...

A 4000Kg4000Kg truck is parked on a 7.0∘{{7.0}^{\circ }} slope. How big is the friction force on the truck?

Explanation

Solution

Let us first analyze all the forces acting on this heavy truck. Since the truck is parked on the incline and is at rest, this means that all the forces acting on the truck are completely balanced by each other. Therefore, balance all the forces after calculating their respective components in the x-direction and y-direction respectively. Then equate the sum of all forces acting in each direction equal to zero.

Complete step-by-step solution:
The forces acting on the truck are namely, gravitational force, normal reaction force and frictional force. Follow the free body diagram of the truck below:

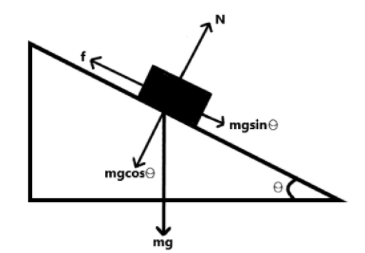
Here, gravitational force acts in the downward direction (=mg), normal reaction force (=N) acts perpendicularly outward to the surface of the incline and friction force (=fs={{f}_{s}}) acts along the incline.

Hence, resolving components of forces, we get
In y-direction, N−mgcos⁡θ=0N-mg\cos \theta =0
⇒N=mgcos⁡θ\Rightarrow N=mg\cos \theta
In x-direction, mgsin⁡θ−fs=0mg\sin \theta -{{f}_{s}}=0
⇒fs=mgsin⁡θ\Rightarrow {{f}_{s}}=mg\sin \theta

Substituting all values in the above equation,
⇒fs=(4000)(9.8)(sin⁡7∘)\Rightarrow {{f}_{s}}=\left( 4000 \right)\left( 9.8 \right)\left( \sin {{7}^{\circ }} \right)

Now, sin⁡7∘≈0.12\sin {{7}^{\circ }}\approx 0.12

& \Rightarrow {{f}_{s}}=\left( 4000 \right)\left( 9.8 \right)\left( 0.12 \right) \\\ & \Rightarrow {{f}_{s}}\approx 4.7\times {{10}^{3}}N \\\ \end{aligned}$$ Therefore, the frictional force acting the truck is approximately $$4.7\times {{10}^{3}}$$ Newton. This type of frictional force is called static frictional force because the object on which it is acting is at rest. **Note:** The frictional force acting on a body in motion is known as the kinetic frictional force. The frictional force acting on a body reaches its maximum value which is called the limiting friction to prevent the body from initiating its motion but if the body overcomes this force then the kinetic frictional force continues to act on the body throughout its motion.