Question

A $400{\text{N}}$ box is suspended motionless from a steel frame by two ropes A and B which hang straight up and down. Identify the correct statements about the tension in the two ropes.
A. The tension in rope A is larger than that in rope B.
B. The tension in rope B is larger than that in rope A.
C. The tension in the two ropes is greater than $400{\text{N}}$ .
D. The tension in the two ropes is less than $400{\text{N}}$ .
E. The tension in the two ropes is equal to $400{\text{N}}$ .

Answer 1

Hint:- The box suspended from the steel frame by two ropes will have the translational forces and rotational force acting on it. However, it is said to remain motionless. This implies that the box is in mechanical equilibrium i.e., it is in rotational as well as translational equilibrium.

Complete step-by-step solution:-
Step 1: Sketch a figure showing the suspended box from the steel frame.

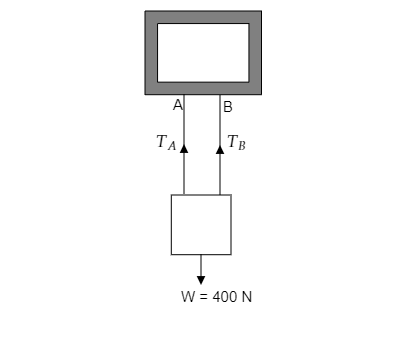
The above figure depicts the box of weight $W = 400{\text{N}}$hanging from a steel frame by two ropes A and B.

Let ${T_A}$ be the tension in the rope A and ${T_B}$ be the tension in the rope B.
Step 2: Based on the fact that the box is motionless, explain the rotational equilibrium of the box.
The two ropes experience a torque as a box of some mass is suspended from the steel frame. But it is said that the suspended box remains motionless. This implies that the total torque acting on the box is zero. And hence the box is in rotational equilibrium. Since the net torque is zero, the tension in both the ropes must be equal i.e., ${T_A} = {T_B} = T$ .
Step 3: Based on the fact that the box is motionless, explain the translational equilibrium of the box.
We have established that the tension in both ropes is the same. The box is also in translational equilibrium as it hangs motionless from the steel frame. This suggests that the net force acting on the suspended box is zero. The translational forces acting on the system are the weight of the box and the tension in the ropes.
Then the force equation can be expressed as $W - \left( {{T_A} + {T_B}} \right) = 0$ or ${T_A} + {T_B} = W$.
Since ${T_A} = {T_B} = T$ we have $2T = W = 400{\text{N}}$ or, $T = 200{\text{N}}$ .
So we conclude that the tension in both ropes will be equal to $W = 400{\text{N}}$ .
Hence the correct option is E.

Note:- Since the two ropes are said to be hanging straight up and down, the tensions in the two ropes will only have vertical components and the net force is taken for the vertical direction. Torque refers to the twisting force acting on a rope as it has a weight hanging from one of its ends. The rest position of the box is what gives rise to its mechanical equilibrium.