Question

A $4{\text{ }}m$ long rod of negligible weight is to be balanced about a point $125{\text{ }}cm$ from its one end. A load of $16{\text{ }}kgf$ is suspended at a point $60{\text{ }}cm$ from the support on the shorter arm.
(a) A weight $W$ is placed $250{\text{ }}cm$ from the support on the longer arm. Find $W$
(b) If $W = 5{\text{ }}kgf$, where must it be kept to balance the rod?

Answer 1

We have to use the concept of torque in this question. As the rod is of negligible mass we have to consider only the weight of the body. It is given at a point where the weight is balanced, so by comparing the torque on the right and left side of the support we will find the answers.

Complete step by step answer:
(a) Torque is defined as a force which has the ability to rotate an object about its axis.According to the given question, the weight of $16{\text{ }}kgf$ is $60{\text{ }}cm$ from the support and the weight $W$ is $125{\text{ }}cm$ from the support. The weight of the rod is negligible, so we did not have to consider it.

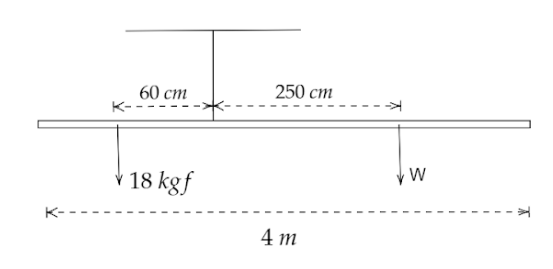
Let the torque on the right side be ${\tau _1}$ and the left side be ${\tau _2}$.
We get, ${\tau _1} = W \times 250$ and ${\tau _2} = 18 \times 60$
In order to balance the rod both the torques are the same.
${\tau _1} = {\tau _2}$
$\Rightarrow W \times 250 = 18 \times 60$
By cross-multiplication we get,
$W = 4.32$
So, the weight $W$ is $4.32{\text{ }}kgf$.

(b) By using the concept of torque we will find the balancing point. According to the given question, the weight of $16{\text{ }}kgf$ is $60{\text{ }}cm$ from the balancing point but a weight $W = 5{\text{ }}kgf$ is introduced.

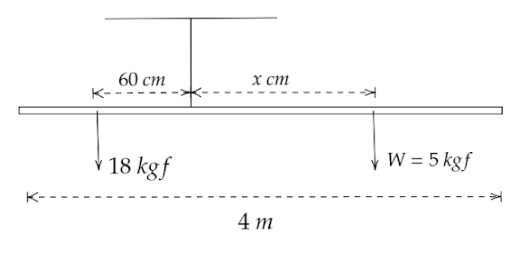
Let the torque on the right side be ${\tau _1}$ and the left side be ${\tau _2}$. Let the length at which the weight is kept for the rod to be balanced be $x$.
We get, ${\tau _1} = 5 \times x$ and ${\tau _2} = 18 \times 60$
In order to balance the rod both the torques are the same.
${\tau _1} = {\tau _2}$
$\Rightarrow x \times 5 = 18 \times 60$
By cross-multiplication we get,
$x = 216$
So, the weight of $5{\text{ }}kgf$ is to be placed $216{\text{ }}cm$ from the balancing point in order to balance the rod.

Note: It must be noted that torque has a $\sin \theta$ component in it too. In this case $\sin \theta = 1$ as the force is acting vertically downwards, so the angle between force and the point of rotation or support is ${90^ \circ }$. And the value of $\sin {90^ \circ } = 1$. The SI unit of torque is newton-meter and it is a vector quantity.