Question

If A (0,α) and B (0,β) , α, β > 0 are two vertices of a variable triangle ABC where the vertex C (x, 0) is variable. The value of x for which ∠ACB is maximum is :

• A. $\frac{α+β}{2}$
• B. $\sqrt{αβ}$
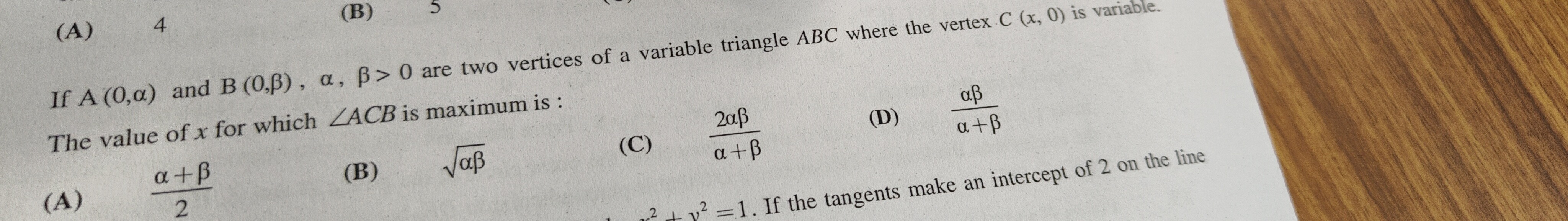
• C. $\frac{2αβ}{α+β}$
• D. $\frac{αβ}{α+β}$

Answer 1

Answer: (B)

$\sqrt{αβ}$

Answer 2

Let the coordinates of the vertices be A(0, α), B(0, β), and C(x, 0). The slope of line AC is $m_1 = \frac{0 - \alpha}{x - 0} = -\frac{\alpha}{x}$. The slope of line BC is $m_2 = \frac{0 - \beta}{x - 0} = -\frac{\beta}{x}$.

Let ∠ACB = θ. The tangent of the angle between two lines is given by: $\tan \theta = \left| \frac{m_2 - m_1}{1 + m_1 m_2} \right|$

Substituting the slopes: $\tan \theta = \left| \frac{-\frac{\beta}{x} - (-\frac{\alpha}{x})}{1 + (-\frac{\alpha}{x})(-\frac{\beta}{x})} \right| = \left| \frac{\frac{\alpha - \beta}{x}}{1 + \frac{\alpha \beta}{x^2}} \right|$ $\tan \theta = \left| \frac{(\alpha - \beta)x}{x^2 + \alpha \beta} \right|$

Assuming α ≠ β (otherwise ∠ACB = 0), and considering x > 0, we have $\tan \theta = \frac{|\alpha - \beta| x}{x^2 + \alpha \beta}$. To maximize ∠ACB, we need to maximize $\tan \theta$. This is equivalent to maximizing the term $\frac{x}{x^2 + \alpha \beta}$. This can be done by minimizing the reciprocal expression $\frac{x^2 + \alpha \beta}{x} = x + \frac{\alpha \beta}{x}$.

Using the AM-GM inequality for $x > 0$: $x + \frac{\alpha \beta}{x} \ge 2 \sqrt{x \cdot \frac{\alpha \beta}{x}}$ $x + \frac{\alpha \beta}{x} \ge 2 \sqrt{\alpha \beta}$

The minimum value of $x + \frac{\alpha \beta}{x}$ is $2 \sqrt{\alpha \beta}$, which occurs when $x = \frac{\alpha \beta}{x}$. $x^2 = \alpha \beta$ $x = \sqrt{\alpha \beta}$ (since we consider x > 0).

Thus, ∠ACB is maximum when $x = \sqrt{\alpha \beta}$.