Solveeit Logo
Login

Question

Question: A thin uniform wire is bent to form the two equal sides AB and AC of triangle ABC, where AB = AC = 5...

A thin uniform wire is bent to form the two equal sides AB and AC of triangle ABC, where AB = AC = 5 cm. The third side BC, of length 6cm, is made from uniform wire of twice the linear mass density of the first. The distance of centre of mass from A is :

A

3411\frac{34}{11} cm

B

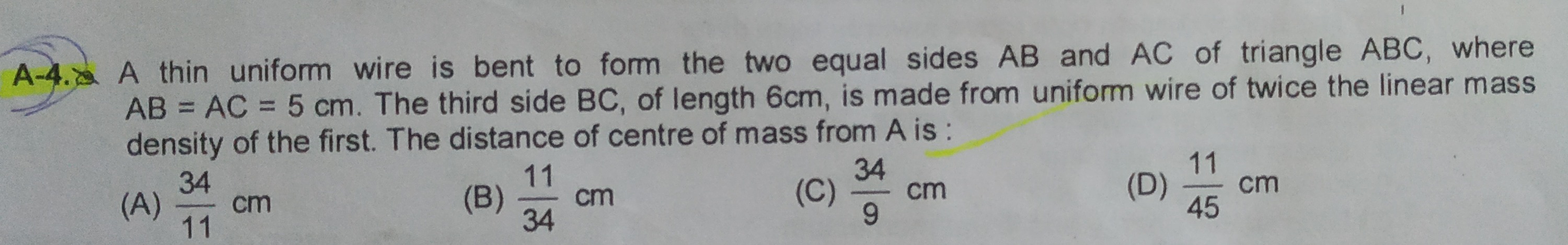
1134\frac{11}{34} cm

C

349\frac{34}{9} cm

D

1145\frac{11}{45} cm

Answer

3411\frac{34}{11} cm

Explanation

Solution

To find the center of mass of the given wire frame, we first need to define a coordinate system and determine the coordinates of the vertices of the triangle.

Let A be the apex of the isosceles triangle ABC. Let D be the midpoint of BC. Then AD is the altitude from A to BC.
Given AB = AC = 5 cm and BC = 6 cm.
In right-angled triangle ADB (or ADC), BD = BC/2 = 6/2 = 3 cm.
The height AD can be found using the Pythagorean theorem: AD=AB2−BD2=52−32=25−9=16=4AD = \sqrt{AB^2 - BD^2} = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4 cm.

Let's place the midpoint D of BC at the origin (0,0) of our coordinate system. Since the triangle is symmetric about the y-axis, A will be on the y-axis.
The coordinates of the vertices are: A = (0, 4)
B = (-3, 0)
C = (3, 0)

Now, let's calculate the mass and the center of mass for each segment of the wire.
Let λ\lambda be the linear mass density of the wire for sides AB and AC.
The linear mass density for side BC is 2λ2\lambda.

  1. Segment AB:
    Length LAB=5L_{AB} = 5 cm.
    Mass mAB=LAB×λ=5λm_{AB} = L_{AB} \times \lambda = 5\lambda.
    The center of mass of a uniform rod is at its midpoint.
    Coordinates of CMAB=(xA+xB2,yA+yB2)=(0+(−3)2,4+02)=(−32,2)CM_{AB} = \left(\frac{x_A + x_B}{2}, \frac{y_A + y_B}{2}\right) = \left(\frac{0 + (-3)}{2}, \frac{4 + 0}{2}\right) = \left(-\frac{3}{2}, 2\right).

  2. Segment AC:
    Length LAC=5L_{AC} = 5 cm.
    Mass mAC=LAC×λ=5λm_{AC} = L_{AC} \times \lambda = 5\lambda.
    Coordinates of CMAC=(xA+xC2,yA+yC2)=(0+32,4+02)=(32,2)CM_{AC} = \left(\frac{x_A + x_C}{2}, \frac{y_A + y_C}{2}\right) = \left(\frac{0 + 3}{2}, \frac{4 + 0}{2}\right) = \left(\frac{3}{2}, 2\right).

  3. Segment BC:
    Length LBC=6L_{BC} = 6 cm.
    Mass mBC=LBC×(2λ)=6×2λ=12λm_{BC} = L_{BC} \times (2\lambda) = 6 \times 2\lambda = 12\lambda.
    Coordinates of CMBC=(xB+xC2,yB+yC2)=(−3+32,0+02)=(0,0)CM_{BC} = \left(\frac{x_B + x_C}{2}, \frac{y_B + y_C}{2}\right) = \left(\frac{-3 + 3}{2}, \frac{0 + 0}{2}\right) = (0, 0).

Now, we calculate the overall center of mass (XCM,YCM)(X_{CM}, Y_{CM}) of the system using the formula:
XCM=mABxAB+mACxAC+mBCxBCmAB+mAC+mBCX_{CM} = \frac{m_{AB}x_{AB} + m_{AC}x_{AC} + m_{BC}x_{BC}}{m_{AB} + m_{AC} + m_{BC}}
YCM=mAByAB+mACyAC+mBCyBCmAB+mAC+mBCY_{CM} = \frac{m_{AB}y_{AB} + m_{AC}y_{AC} + m_{BC}y_{BC}}{m_{AB} + m_{AC} + m_{BC}}

Total mass M=mAB+mAC+mBC=5λ+5λ+12λ=22λM = m_{AB} + m_{AC} + m_{BC} = 5\lambda + 5\lambda + 12\lambda = 22\lambda.

XCM=5λ(−32)+5λ(32)+12λ(0)22λ=−152λ+152λ+022λ=022λ=0X_{CM} = \frac{5\lambda \left(-\frac{3}{2}\right) + 5\lambda \left(\frac{3}{2}\right) + 12\lambda (0)}{22\lambda} = \frac{-\frac{15}{2}\lambda + \frac{15}{2}\lambda + 0}{22\lambda} = \frac{0}{22\lambda} = 0.

YCM=5λ(2)+5λ(2)+12λ(0)22λ=10λ+10λ+022λ=20λ22λ=1011Y_{CM} = \frac{5\lambda (2) + 5\lambda (2) + 12\lambda (0)}{22\lambda} = \frac{10\lambda + 10\lambda + 0}{22\lambda} = \frac{20\lambda}{22\lambda} = \frac{10}{11}.

So, the center of mass of the entire wire frame is (0,1011)(0, \frac{10}{11}).

The question asks for the distance of the center of mass from A.
A is at (0,4)(0,4).
The center of mass is at (0,1011)(0, \frac{10}{11}).
Since both points lie on the y-axis, the distance between them is the absolute difference of their y-coordinates.
Distance d=∣yA−YCM∣=∣4−1011∣=∣4×11−1011∣=∣44−1011∣=3411d = |y_A - Y_{CM}| = \left|4 - \frac{10}{11}\right| = \left|\frac{4 \times 11 - 10}{11}\right| = \left|\frac{44 - 10}{11}\right| = \frac{34}{11} cm.