Question

A (4, -6), B(3,-2) and C(5, 2) are the verticals of a $\vartriangle$ABC and AD is its median. Prove that the median AD divide $\vartriangle$ABC into two triangles of equal areas.

Answer 1

In this question first we have to draw the diagram with the help of three coordinates A (4, -6), B(3,-2) and C(5, 2) that is forming a triangle in which AD is the median. We have to use the formula of finding the coordinates of D $(x,y) = (\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2})$.

Complete step-by-step answer:
We have AD as median in the triangle ABC
First, we have to find the coordinates of point D that lies on the line BC
Formula of finding the coordinates of point D $(x,y) = (\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2})$
Here we
${x_1} = 3$
${x_2} = 5$
${y_1} = - 2$
${y_2} = 2$
Putting values in the formula
$= (\dfrac{{3 + 5}}{2},\dfrac{{ - 2 + 2}}{2})$
$= (\dfrac{8}{2},\dfrac{0}{2})$
Dividing the numerator by denominator
$= (4,0)$
Here we have the point D $(4,0)$

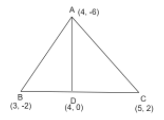
To prove the AD is the median of the triangle we have to prove that area of triangle ABD is equal to area of triangle ACD.
Area of triangle ABD = Area of triangle ACD
Formula of finding the area of triangle using the three coordinates is
$\dfrac{1}{2}\\{ Ax(By - Cy) + Bx(Cy - Ay) + Cx(Ay - By)\\}$
Simply put the values of coordinates in the formula
In triangle ABD & triangle ACD
$\Rightarrow$ $\dfrac{1}{2}(4(0 - ( - 2)) + 4( - 2 - ( - 6)) + 3( - 6 - 0))$

$\Rightarrow$ $\dfrac{1}{2}(4(0 + 2) + 4(-2 + 6) + 3( - 6 - 0))$

$\Rightarrow$ $\dfrac{1}{2}(8 + 16 - 18)$

$\Rightarrow$ $\dfrac{1}{2}( - 8 + 32 - 30)$
Simplify the equation
$\Rightarrow$ $\dfrac{1}{2}.6 = \dfrac{1}{2}. - 6$
$\Rightarrow$ $3 = - 3$
The area of triangle ABD is 3 square unit and the area of triangle ACD is -3 square unit
Because the area cannot be negative so the area of triangle ACD is 3 square units.
Hence both triangles having the equal area so, proven that AD is the median of triangle ABC.

Note: First find the coordinates of the point D and then find the area of both the triangles always make the diagram to understand the coordinates here students get confused between the coordinates.