Question

A 384- square-meter plot of land is to be enclosed by a fence and divided into two equal parts by another fence parallel to one pair of sides. What dimensions of the outer rectangle will minimize the amount of fence used?

Answer 1

Hint : In this question, we need to determine the dimensions of the outer rectangle will minimize the amount of fence used such that the rectangular plot is divided into two parts by fencing across either of the parallel sides of the rectangular plot. For this, we will establish a relation between the total lengths of the fence used for fencing the rectangular plot and then, differentiate the equation.

Complete step-by-step answer :
Let the length of the rectangular plot be $l{\text{ meters}}$ , and the width of the rectangular plot be $w{\text{ meters}}$.
The product of the length and the width of the rectangle results in the area of the rectangle. Mathematically, $A = l \times w$.
According to the question, the area of the rectangular plot is 384- square-meters.
So, substituting $A = 384{\text{ }}{{\text{m}}^2}$ in the equation $A = l \times w$ we get
$384 = l \times w - - - - (i)$
From equation (i), we can write the expression for the width of the rectangular plot as:
$384 = l \times w \\\ w = \dfrac{{384}}{l} - - - - (ii) \\\$
Now, as the rectangular field has been divided into two equal parts by fencing the plot in between either across the length or the width.
So, let us consider that the rectangular plot has been divided into two parts by fencing the plot parallel to the width of the plot.

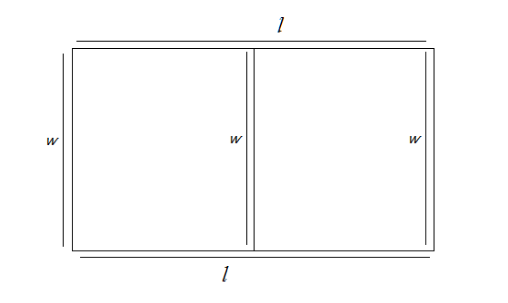
Also, let us consider that the total length of the fence required to enclose the plot and divide the plot in two equal half be $x$.
Then, from the figure, we can see that the total length of the fence required will be $\left( {2l + 3w} \right)$ which is equivalent to $x$. Hence, we can write
$x = 2l + 3w - - - - (iii)$
Substituting the value of the width of the rectangle from the equation (ii) in the equation (iii) we get
$x = 2l + 3\left( {\dfrac{{384}}{l}} \right) \\\ x = 2l + \dfrac{{1152}}{l} - - - - (iv) \\\$
Now, differentiate equation (iv) with respect to the length of the rectangular field, we get
$\dfrac{{dx}}{{dl}} = \dfrac{d}{{dl}}\left( {2l + \dfrac{{1152}}{l}} \right) \\\ = 2 - \dfrac{{1152}}{{{l^2}}} - - - - (v) \\\$
To get the maximum value of the sides of the rectangular field so as to minimize the amount of the fence used will be calculated by equating $\dfrac{{dx}}{{dl}}$ to zero.
$\dfrac{{dx}}{{dl}} = 0 \\\ 2 - \dfrac{{1152}}{{{l^2}}} = 0 \\\ 2 = \dfrac{{1152}}{{{l^2}}} \\\ {l^2} = \dfrac{{1152}}{2} \\\ l = \sqrt {576} \\\ = 24{\text{ meters}} \\\$

Substituting the value of the length of the rectangular plot as 24 meters in the equation (ii), we get
$w = \dfrac{{384}}{l} \\\ = \dfrac{{384}}{{24}} \\\ = 16{\text{ meters}} \\\$
Hence, the dimensions of the outer rectangle will minimize the amount of fence used is $24{\text{ m}} \times 16{\text{ m}}$.

Note : Students must be careful while calculating the total length of the fence required as here we have considered that the fence is used parallel to the width of the rectangular plot so as to divide the area of the plot in two equal halves. Students can also take this as parallel to the length of the rectangular plot so that the equation will become $x = 3l + 2w$ and rest all the process is the same.