Question

A 35m long ladder just reaches a window of a building. If the ladder makes an angle $\theta$ with the level ground, such that $\tan \theta = \dfrac{1}{{2\sqrt 6 }}$ . Find the:
$\left( a \right)$ Height of the window above the ground level and
$\left( b \right)$ The horizontal distance of the foot of the ladder from the building.A

Answer 1

Here in this question we have to find $AC$ and $BC$ for this, we will use the concept of the Pythagoras theorem which is given by $A{B^2} = A{C^2} + B{C^2}$ for this we will find $BC$ by using the value given to us which is given as $\tan \theta = \dfrac{1}{{2\sqrt 6 }}$ .

Formula used:
Pythagoras theorem,
If $AB,BC,AC$ be the sides of the right-angled triangle the Pythagoras theorem is given by
$A{B^2} = A{C^2} + B{C^2}$
Here, $AB,BC,AC$ are the three sides in which $AB$ , will be the hypotenuses and $BC$ will be the base, and $AC$ will be the height of it.

Complete step-by-step answer:
So first of all we will suppose the window will be $A$ and the ladder will be $AB$ .

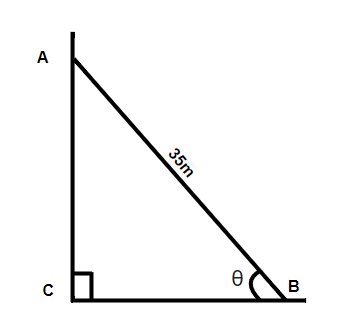
Since,
$\tan \theta = \dfrac{1}{{2\sqrt 6 }}$
So, from the figure, it can be written as
$\Rightarrow \tan \theta = \dfrac{1}{{2\sqrt 6 }} = \dfrac{{AC}}{{BC}}$
And on solving for the value of $BC$ , we get
$\Rightarrow BC = AC \times 2\sqrt 6$ , and we will name it equation $1$
Or it can also be written as
$\Rightarrow {\left( {BC} \right)^2} = 24{\left( {AC} \right)^2}$
So by using the Pythagoras theorem, we have
$A{B^2} = A{C^2} + B{C^2}$
So, on substituting the values we get
$\Rightarrow {\left( {35} \right)^2} = {\left( {AC} \right)^2} + 24{\left( {AC} \right)^2}$
So on solving it, we get
$\Rightarrow 35 \times 35 = 25{\left( {AC} \right)^2}$
Now on multiplying and taking the constant term one side, we get
$\Rightarrow {\left( {AC} \right)^2} = \dfrac{{35 \times 35}}{{25}}$
And on solving furthermore, we get
$\Rightarrow {\left( {AC} \right)^2} = 49$
Therefore, on removing the square, we get
$\Rightarrow AC = 7$
Hence, the height of the window above the ground level will be of $7m$
Now putting this above value in the equation $1$ , we get
$\Rightarrow BC = AC \times 2\sqrt 6$
And on substituting the values, we get
$\Rightarrow BC = 7 \times 2\sqrt 6$
And on solving it we get
$\Rightarrow BC = 14\sqrt 6$
Hence, the horizontal distance of the foot of the ladder from the building will be $14\sqrt 6$ .

Note: For solving this type of question figure also plays an important role for both the invigilator and student to understand quickly and make the solution error-free. So we should always mention the figure in this type of question during the exams especially.