Question

Let $\vec{a}$ = i-2j+k and $\vec{b}$ = i-j+k be two vectors. If $\vec{c}$ is a vector such that $\vec{b}$x$\vec{c}$ = $\vec{b}$x$\vec{a}$ and $\vec{c}$.$\vec{a}$ = 0 then $\vec{c}$.$\vec{b}$ is equal to

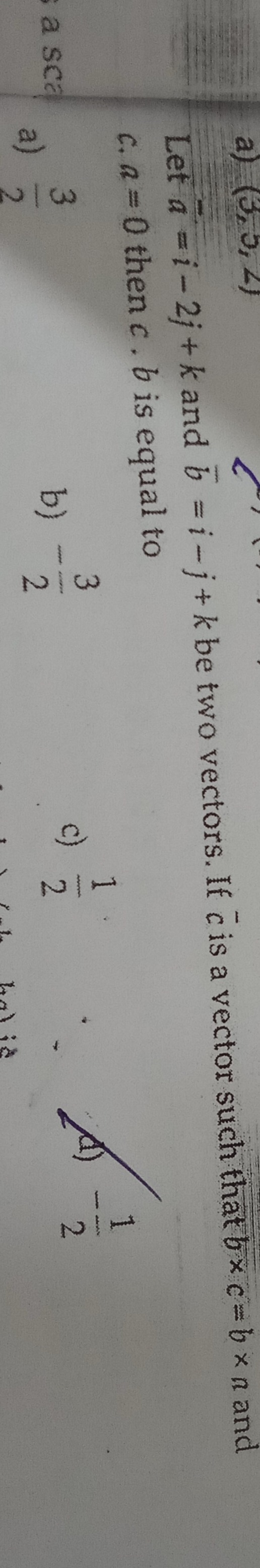
• A. $\frac{3}{2}$
• B. -$\frac{3}{2}$
• C. $\frac{1}{2}$
• D. -$\frac{1}{2}$

Answer 1

Answer: (D)

-$\frac{1}{2}$

Answer 2

Given

$$\vec{a} = i - 2j + k,\quad \vec{b} = i - j + k$$

and conditions

$$\vec{b} \times \vec{c} = \vec{b} \times \vec{a} \quad \text{and} \quad \vec{c}\cdot \vec{a} = 0.$$

Since

$$\vec{b} \times \vec{c} = \vec{b} \times \vec{a} \implies \vec{b} \times (\vec{c}-\vec{a}) = \vec{0},$$

we conclude that

$$\vec{c}-\vec{a} = \lambda \vec{b} \quad \text{or} \quad \vec{c} = \vec{a} + \lambda \vec{b}.$$

Using $\vec{c}\cdot\vec{a} = 0$:

$$(\vec{a} + \lambda \vec{b})\cdot \vec{a} = 0 \implies \vec{a}\cdot\vec{a} + \lambda (\vec{a}\cdot\vec{b}) = 0.$$

Compute:

$$\vec{a}\cdot\vec{a} = 1^2 + (-2)^2 + 1^2 = 6, \quad \vec{a}\cdot\vec{b} = (1)(1) + (-2)(-1) + (1)(1) = 4.$$

Thus,

$$6 + 4\lambda = 0 \implies \lambda = -\frac{6}{4} = -\frac{3}{2}.$$

Now, find $\vec{c}\cdot \vec{b}$:

$$\vec{c}\cdot\vec{b} = (\vec{a} + \lambda \vec{b})\cdot \vec{b} = \vec{a}\cdot\vec{b} + \lambda (\vec{b}\cdot\vec{b}).$$

We already have $\vec{a}\cdot\vec{b}=4$. Also,

$$\vec{b}\cdot\vec{b} = 1^2 + (-1)^2 + 1^2 = 3.$$

Thus,

$$\vec{c}\cdot\vec{b} = 4 + \left(-\frac{3}{2}\right)(3) = 4 - \frac{9}{2} = \frac{8-9}{2} = -\frac{1}{2}.$$