Solveeit Logo
Login

Question

Question: A 32 kg disc moving with the velocity \(v=25m/s\) toward the two stationary discs of mass 8 kg on a ...

A 32 kg disc moving with the velocity v=25m/sv=25m/s toward the two stationary discs of mass 8 kg on a frictionless surface. The discs collide elastically. After the collision, the heavy disc is at rest and the two smaller discs scatter outward at the same speed. What is the x-component of the velocity of each of the 8 kg discs in the final state?

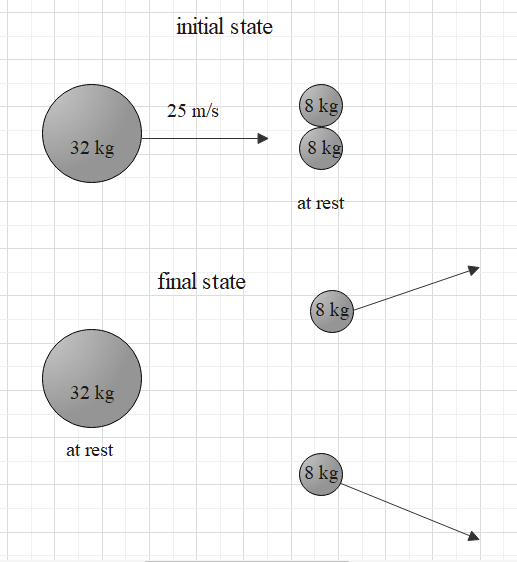
a) 12.5 m/s
b) 16 m/s
c) 25 m/s
d) 50 m/s
e) 100 m/s

Explanation

Solution

By applying conservation of momentum formula for the initial and final conditions given: (m1v1+m2v2)initial=(m1v1+m2v2)final{{\left( {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \right)}_{initial}}={{\left( {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \right)}_{final}} and find final velocity.

Complete step by step answer:
We have the following data:
m1=32kg m2=8kg m3=8kg \begin{aligned} & {{m}_{1}}=32kg \\\ & {{m}_{2}}=8kg \\\ & {{m}_{3}}=8kg \\\ \end{aligned}
Initial condition:
v1=25m/s v2=v3=0 \begin{aligned} & {{v}_{1}}=25m/s \\\ & {{v}_{2}}={{v}_{3}}=0 \\\ \end{aligned}
Fina condition:
v1=0 v2=v3=v \begin{aligned} & {{v}_{1}}=0 \\\ & {{v}_{2}}={{v}_{3}}=v \\\ \end{aligned}
So, by applying the conservation of momentum formula:
(m1v1+m2v2)initial=(m1v1+m2v2)final{{\left( {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \right)}_{initial}}={{\left( {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \right)}_{final}}
We get:

\left( 32\times 25 \right)+\left( 8\times 0 \right)+\left( 8\times 0 \right)=\left( 32\times 0 \right)+\left( 8\times v \right)+\left( 8\times v \right) \\\
\implies 800+0+0=0+8v+8v \\\
  ⟹  800=16v v=50m/s\implies 800=16v \\\ v=50m/s
Therefore, the x-component of the velocity of each of the 8 kg discs in the final state is 50 m/s.

So, the correct answer is “Option D”.

Note:
The conservation of momentum states that, within some problem domain, the amount of momentum remains constant; momentum is neither created nor destroyed, but only changed through the action of forces as described by Newton's laws of motion.
An elastic collision is a collision in which there is no net loss in kinetic energy in the system as a result of the collision. Both momentum and kinetic energy are conserved quantities in elastic collisions.
Therefore, we can solve the given question by conservation of energy also.