Question

Let $\overrightarrow{V}=2\hat{i}+\hat{j}-\hat{k}$, $\overrightarrow{W}=\hat{i}+3\hat{k}$, $|\overrightarrow{U}|=2$. If $\overrightarrow{U}$ is a vector in x-y plane, then greatest value of $([\overrightarrow{U}\overrightarrow{V}\overrightarrow{W}])^2$ is -

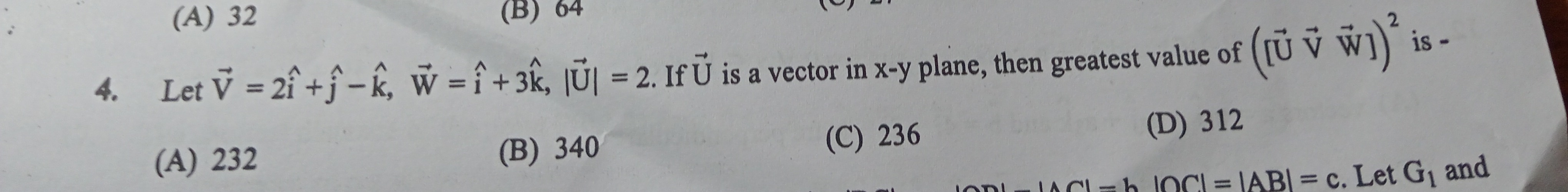
• A. 232
• B. 340
• C. 236
• D. 312

Answer 1

Answer: (A)

232

Answer 2

The scalar triple product $[\overrightarrow{U}\overrightarrow{V}\overrightarrow{W}]$ is given by $\overrightarrow{U} \cdot (\overrightarrow{V} \times \overrightarrow{W})$.

First, calculate the cross product $\overrightarrow{V} \times \overrightarrow{W}$: $\overrightarrow{V} = 2\hat{i}+\hat{j}-\hat{k}$ $\overrightarrow{W} = \hat{i}+3\hat{k} = \hat{i}+0\hat{j}+3\hat{k}$ $\overrightarrow{V} \times \overrightarrow{W} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & -1 \\ 1 & 0 & 3 \end{vmatrix} = \hat{i}(1 \cdot 3 - (-1) \cdot 0) - \hat{j}(2 \cdot 3 - (-1) \cdot 1) + \hat{k}(2 \cdot 0 - 1 \cdot 1)$ $= \hat{i}(3) - \hat{j}(6 + 1) + \hat{k}(0 - 1) = 3\hat{i} - 7\hat{j} - \hat{k}$.

Let $\overrightarrow{P} = \overrightarrow{V} \times \overrightarrow{W} = 3\hat{i} - 7\hat{j} - \hat{k}$. We are given that $\overrightarrow{U}$ is a vector in the x-y plane and $|\overrightarrow{U}| = 2$. Let $\overrightarrow{U} = u_x\hat{i} + u_y\hat{j}$. The condition $|\overrightarrow{U}| = 2$ means $\sqrt{u_x^2 + u_y^2} = 2$, or $u_x^2 + u_y^2 = 4$.

The scalar triple product is $[\overrightarrow{U}\overrightarrow{V}\overrightarrow{W}] = \overrightarrow{U} \cdot \overrightarrow{P} = (u_x\hat{i} + u_y\hat{j}) \cdot (3\hat{i} - 7\hat{j} - \hat{k})$ $= u_x(3) + u_y(-7) + 0(-1) = 3u_x - 7u_y$.

We want to find the greatest value of $([\overrightarrow{U}\overrightarrow{V}\overrightarrow{W}])^2 = (3u_x - 7u_y)^2$, subject to the constraint $u_x^2 + u_y^2 = 4$.

We can use the Cauchy-Schwarz inequality. For two vectors $\vec{a} = (a_1, a_2)$ and $\vec{b} = (b_1, b_2)$, $(\vec{a} \cdot \vec{b})^2 \le |\vec{a}|^2 |\vec{b}|^2$. Let $\vec{a} = (u_x, u_y)$ and $\vec{b} = (3, -7)$. Then $\vec{a} \cdot \vec{b} = 3u_x - 7u_y$. $|\vec{a}|^2 = u_x^2 + u_y^2 = 4$. $|\vec{b}|^2 = 3^2 + (-7)^2 = 9 + 49 = 58$.

Applying the Cauchy-Schwarz inequality: $(3u_x - 7u_y)^2 \le (u_x^2 + u_y^2)(3^2 + (-7)^2)$ $(3u_x - 7u_y)^2 \le (4)(58)$ $(3u_x - 7u_y)^2 \le 232$.

The maximum value of $(3u_x - 7u_y)^2$ is 232.

Alternatively, using parametrization: Let $u_x = 2\cos\theta$ and $u_y = 2\sin\theta$. $3u_x - 7u_y = 3(2\cos\theta) - 7(2\sin\theta) = 6\cos\theta - 14\sin\theta$. The expression $a\cos\theta + b\sin\theta$ has a maximum value of $\sqrt{a^2 + b^2}$ and a minimum value of $-\sqrt{a^2 + b^2}$. Here, $a=6$ and $b=-14$. The maximum value of $6\cos\theta - 14\sin\theta$ is $\sqrt{6^2 + (-14)^2} = \sqrt{36 + 196} = \sqrt{232}$.

So, the value of $(3u_x - 7u_y)^2$ ranges from $0$ to $(\sqrt{232})^2 = 232$. The greatest value is 232.