Question

A 30V, 90W lamp is to be operated on a 120V DC line. For a proper glow, a resistor of ….. should be connected in series with the lamp.
A) 10
B) 20
C) 30
D) 40

Answer 1

Here we have given a lamp of voltage 30V and power 90W connected to a DC line which has voltage of 120V. The power is given as product of voltage and current and according to Ohm’s law the voltage is given as product of current and resistance. By using these two formulas we can solve the above question.

Formula used:

& P=VI \\\ & V=IR \\\ & R={{R}_{1}}+{{R}_{2}} \\\ \end{aligned}$$ **Complete step by step answer:** The circuit diagram for the question can be given as follows 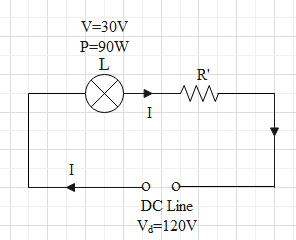 Where L is the lamp having voltage of 30V and power 90W, R’ is the resistor connected in series for proper glow and I is the current flowing through the circuit. As some current is flowing through the lamp then there will be resistance too which will try to oppose the flow. Let us first find the resistance of the lamp. The power is given as the product of voltage and the current, $$P=VI\text{ }.............\text{(i)}$$ Now according to Ohm’s law the voltage across the device will be proportional to the current and it is given as $$\begin{aligned} & V=IR \\\ & \Rightarrow I=\dfrac{V}{R}\text{ }...............\text{(ii)} \\\ \end{aligned}$$ Here we have to calculate the resistance of the lamp and the given data for the lamp are voltage and power. So we need a formula of resistance in terms of power and voltage. Substituting value of I from equation (ii) in equation (i), we get $$\begin{aligned} & P=V\left( \dfrac{V}{R} \right) \\\ & \Rightarrow P=\dfrac{{{V}^{2}}}{R} \\\ & \Rightarrow R=\dfrac{{{V}^{2}}}{P} \\\ \end{aligned}$$ Substituting the value of voltage and power of the lamp, $$V=30V,P=90W$$ $$\begin{aligned} & R=\dfrac{{{\left( 30 \right)}^{2}}}{90} \\\ & \Rightarrow R=\dfrac{900}{90} \\\ & \Rightarrow R=10\Omega \\\ \end{aligned}$$ Now, from equation (ii) the current flowing through the lamp is given as $$\begin{aligned} & I=\dfrac{V}{R} \\\ & I=\dfrac{30}{10} \\\ & I=3A \\\ \end{aligned}$$ Let us consider the DC line, it will have resistance too, and the current flowing through it will be same as the current flowing through lamp, if the voltage of the DC line is $${{V}_{d}}$$, then the resistance for the DC line can be given as $${{R}_{d}}=\dfrac{{{V}_{d}}}{I}\text{ }\left( \because {{V}_{d}}=I{{R}_{d}} \right)$$ Substituting$${{V}_{d}}=120V\text{ and }I=3A$$, we get $$\begin{aligned} & {{R}_{d}}=\dfrac{120}{3} \\\ & {{R}_{d}}=40\Omega \\\ \end{aligned}$$ The question says that a resistor should be added in series with the lamp for a proper glow, i.e. a resistor should be added in series with the resistor of the lamp so the equivalent resistor will be given by the resistance of the DC line. If R’ is the resistor added, then $$\begin{aligned} & {{R}_{d}}=R'+R \\\ & \Rightarrow R'={{R}_{d}}-R \\\ & \Rightarrow R'=40-10 \\\ & \Rightarrow R'=30\Omega \\\ \end{aligned}$$ Hence, for a proper glow of lamp a $$30\Omega $$resistor should be connected in series with the lamp. **Therefore option C is correct.** **Note:** The resistance of the lamp and the resistance of the lamp is added as they are connected in series. In case the external resistor was connected in parallel then the formula for the parallel combination of resistance should be used where the equivalent resistance will be given by DC line. The equivalent resistance is given by the DC line as the main current is flowing through it.