Question

A $3\Omega$ resistor and a $6\Omega$ resistor are connected in parallel and the combination is connected in series to a battery of 5V and a $3\Omega$ resistor. The potential difference across the $6\Omega$ resistor

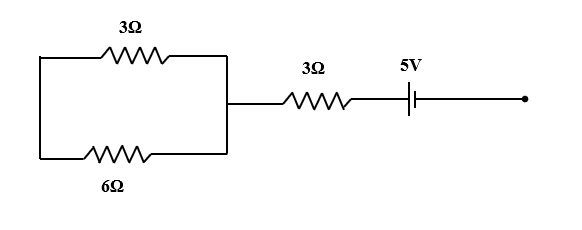
A. 2V
B. 4V
C. 3V
D. 1V

Answer 1

To solve this problem, first find the equivalent resistance across $3\Omega$ and $6\Omega$ resistors. Then, find the total resistance in the circuit. Substitute the total resistance and the voltage of the batter in the formula for Ohm’s law. This will give the current flowing through the circuit. Then, find the current passing through $6\Omega$ resistor. Now, using this obtained current across $6\Omega$ resistor, find the potential difference across $6\Omega$ resistor.

Complete answer:
Given: ${ R }_{ 1 }=3\Omega$
${ R }_{ 2 }=6\Omega$
${ R }_{ 1 }=3\Omega$
Voltage (V)= 5V
Resistors ${ R }_{ 1 }$ and ${ R }_{ 2 }$ are connected in parallel.
So, the equivalent resistance in the combination is given by,
$\dfrac { 1 }{ { R }_{ eq } } =\dfrac { 1 }{ { R }_{ 1 } } +\dfrac { 1 }{ { R }_{ 2 } }$
Substituting the values we get,
$\dfrac { 1 }{ { R }_{ eq } } =\dfrac { 1 }{ 3 } +\dfrac { 1 }{ 6 }$
$\Rightarrow \dfrac { 1 }{ { R }_{ eq } } =\dfrac { 9 }{ 18 }$
$\Rightarrow { R }_{ eq }=\dfrac { 18 }{ 9 }$
$\therefore {R}_{eq} = 2\Omega$
Therefore, the total resistance in the circuit is,
$R= {R}_{eq}+ {R}_{3}$
Substituting the values we get,
$R= 2 + 3$
$\Rightarrow R= 5\Omega$
Using Ohm’s Law,
$V=IR$
Substituting the values we get,
$5= I \times 5$
$\Rightarrow I =1A$
Current flowing through $6\Omega$ resistor is given by,
${ I }^{ ' }=\dfrac { { R }_{ 3 } }{ { R }_{ 3 }+{ R }_{ 2 } } I$
Substituting the values in above expression we get,
${ I }^{ ' }=\dfrac { 3 }{ 3+6 } \times 1$
$\Rightarrow { I }^{ ' }=\dfrac { 3 }{ 9 }$
$\Rightarrow { I }^{ ' }=\dfrac { 1 }{ 3 }$
Voltage across $6\Omega$ resistor is given by,
${ V }^{ ' }={ I }^{ ' }\times { R }_{ 2 }$
Substituting the values in above equation we get,
${ V }^{ ' }=\dfrac { 1 }{ 3 } \times 6$
$\therefore { V }^{ ' }= 2V$
Hence, the potential difference across the $6\Omega$ resistor is 2V.

So, the correct answer is “Option A”.

Note:
Students generally get confused between the formula for equivalent resistance in parallel combination and series combination & the equivalent capacitance in series and parallel combination. So, they should clearly know these formulas to solve these types of problems. Students should also remember that the equivalent resistance of a combination is always less than the smallest resistance in the parallel network.