Question

A $2m$ wide truck is moving with a uniform speed ${v_0} = 8m{s^{ - 1}}$ along a straight horizontal road. A pedestrian starts to cross the road with a uniform speed $v$ , when the truck is $4m$ away from him. The minimum value of $v$ so that he can cross the road safely is
(A) $2.62m{s^{ - 1}}$
(B) $4.6m{s^{ - 1}}$
(C) $3.57m{s^{ - 1}}$
(D) $1.414m{s^{ - 1}}$

Answer 1

Hint : To solve this question, we need to find the time required for the total width of the truck to pass through the road. Then, we have to equate it to the time required by the pedestrian to cross the road, to get the required value of minimum velocity.

Complete step by step answer
Let the pedestrian move at an angle of ${\theta}$ with the horizontal, as shown in the following figure.

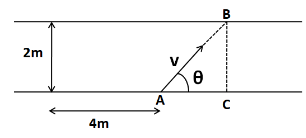
As the width of the truck is equal to $2m$ , so the pedestrian has to cross a vertical distance of $2m$ on the road. Resolving the velocity of the pedestrian into vertical direction, we get
$\Rightarrow {v_y} = v\sin {\theta}$
The vertical distance will be covered by this component of the velocity of the pedestrian. So the time required for this is given by
$\Rightarrow t = \dfrac{2}{{v\sin {\theta}}}$ ……………………..(1)
From the triangle ABC in the above figure, we have
$\Rightarrow \tan {\theta} = \dfrac{{BC}}{{AC}}$
$\Rightarrow AC = BC\cot {\theta}$
From the above figure, $BC = 2m$ . So we have
$\Rightarrow AC = 2\cot {\theta}$ ……………………..(2)
Now, the total horizontal distance covered by the truck, if the velocity of the pedestrian is just sufficient to cross the road safely is given by
$\Rightarrow x = 4 + AC$
From (2)
$\Rightarrow x = 4 + 2\cot {\theta}$ ……………………..(3)
As the truck is moving with a speed of ${v_0} = 8m{s^{ - 1}}$ so the time required for it to cover this horizontal distance is given by
$\Rightarrow t = \dfrac{x}{{{v_0}}}$
$\Rightarrow t = \dfrac{{4 + 2\cot {\theta}}}{8}$ ……………………..(4)
Equating (1) and (4) we get
$\Rightarrow \dfrac{2}{{v\sin {\theta}}} = \dfrac{{4 + 2\cot {\theta}}}{8}$
On cross multiplying, we get
$\Rightarrow v\sin {\theta}\left( {4 + 2\cot {\theta}} \right) = 16$
$\Rightarrow v = \dfrac{{16}}{{4\sin {\theta} + 2\cos {\theta}}}$ ……………………..(5)
For minimum velocity of the pedestrian, the denominator must be maximum, which is given by
$\Rightarrow D = 4\sin {\theta} + 2\cos {\theta}$
As it is maximum, so we have
$\Rightarrow \dfrac{{dD}}{{d{\theta}}} = 0$
$\Rightarrow 4\cos {\theta} - 2\sin {\theta} = 0$
On simplifying, we get
$\Rightarrow \tan {\theta} = 2$
From this value, it is easy to obtain
$\Rightarrow \sin {\theta} = \dfrac{2}{{\sqrt 5 }}$ ……………………..(6)
$\Rightarrow \cos {\theta} = \dfrac{1}{{\sqrt 5 }}$ ……………………..(7)
Substituting (6) and (7) in (5) we get
$\Rightarrow v = \dfrac{{16\sqrt 5 }}{{10}}$
$\Rightarrow v = 3.57m/s$
Thus the minimum velocity of the pedestrian required to cross the road safely is equal to $3.57m{s^{ - 1}}$ .
Hence, the correct answer is option C.

Note
We should not take the velocity of the pedestrian to be in the vertical direction. As the truck is moving towards the pedestrian, he has to run away from the truck also, along with crossing the road.