Question

A 2m long wooden plank of mass 20 kg is pivoted (supported from below) at 0.5 m from either end. A person of mass 40 kg starts walking from one of these pivots to the farther end. How far can the person walk before the plank topples?

Answer 1

The plank topples when a torque is exerted on the plank due to weight of the person. The torque due to the weight of the rod balances the torque due to weight of man. By equating the expressions for torque for unknown value of distance, we can obtain the required answer.

Formula used:
The expression for torque is given as
$\tau = r \times F$
Here F represents the force applied and r is the distance of the force from the axis of rotation.

Complete step by step answer:
First we need to draw a free body diagram for the wooden plank given in the question. Based on the given information, we have the following configuration.

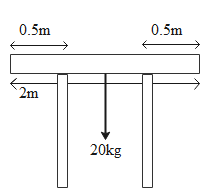
The length of the plank is 2m while the mass of the plank is 20kg and there are two pivots supporting it each at a distance of 0.5m from each end.
Now a man who has a mass of 40kg starts to walk from one of the pivots (let that pivot be the second one in the figure). At a certain point the plank will topple due to the weight of the man. The toppling occurs because a torque is exerted by the weight of the man when its value exceeds the weight of the rod.
Let x be the distance from the centre of the rod towards right at which the torque balances the torque due to weight of the rod.
Therefore, we can write the following expression.
$20g \times 0.5m = 40g \times x \\\ \Rightarrow x = 0.25m \\\$
This is the distance from the centre and the actual distance on the rod is equal to $1 + 0.25 = 1.25m$.

Hence, the rod topples at a distance of 1.25m from the opposite end.

Note: 1. The torque is equal to the product of force and the distance. This means that its magnitude depends on the distance of man from the end of the rod.
2. The axis of rotation here is the end towards which the man moves from a pivot.