Question

A 2kg stone at the end of a string 1m long is whirled in a vertical circle. At some point its speed is 4m/s. The tension of the string is 51.6N. At this instant the stone is:
A. at the top of the circle
B. at the bottom of the circle
C. half way down
D. none of these

Answer 1

Assume that the stone makes an angle θ with vertical. Now, find out all the forces acting on the stone at that instant. Also, resolve the forces acting as per requirement. Since, the stone stays in the circular path without being pulled inward or outward, the forces acting towards the centre and outwards are balanced. You could equate these forces to find θ and hence determine the position of the stone at that particular instant.

Formula used:
Expression for centrifugal force,
${{F}_{c}}=\dfrac{m{{v}^{2}}}{r}$

Complete step-by-step answer:
In the question, we are given a stone that weighs 2kg. This stone is attached at the end of a string that is 1m long and is whirled around in a vertical circle. We are given a particular point at which the speed of the stone is 4m/s and the tension acting in the string towards the centre is 51.6N. We are supposed to find the position of the stone at that particular instant.
Let θ be the angle made by the stone with the vertical at that particular instant.

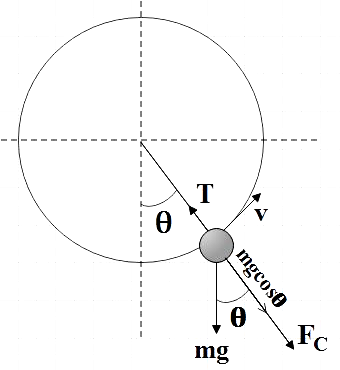
There are mainly three forces that are acting on the stone at that particular instant. First one is the tension T in the string that is acting towards the centre. Next we have the weight of the body acting vertically downward due to gravity. Since the above motion is circular, the third force is the centrifugal force acting on the stone.
Resolving the force due to gravity (weight) into its components, we get $mg\cos \theta$component acting along the same direction as the centrifugal force.
As the stone is not being pulled off from the circular path, it clearly implies that the tension balances the $mg\cos \theta$component and the centrifugal force. That is,
$T={{F}_{c}}+mg\cos \theta$……………………….. (1)
But we know that the expression for centrifugal force is given by,
${{F}_{c}}=\dfrac{m{{v}^{2}}}{r}$
From the question, m=2kg
V=4m/s
r = length of the string=1m
T=51.6N
$\Rightarrow {{F}_{C}}=\dfrac{2\times {{\left( 4 \right)}^{2}}}{1}=32N$………………… (2)
Substituting (2) and also other given values in (1),
$51.6N=32N+2\left( 9.8 \right)\cos \theta$
$\Rightarrow 19.6\cos \theta =19.6$
$\Rightarrow \cos \theta =\dfrac{19.6}{19.6}=1$
$\Rightarrow \theta ={{\cos }^{-1}}\left( 1 \right)=0$
That is the angle made by the stone with the vertical at that instant is zero or in other words the stone was along the vertical. Clearly, the stone at that instant is in the bottom half of the circle.
So, the correct answer is “Option B”.

Note: Whenever we are dealing with motion of a body in more than one dimension, try to resolve the vectors as per requirement. Also, remember that if the body doesn’t show displacement in either direction then the forces acting on the body from both sides are balanced. The centrifugal force actually is a frictional force, that is, in real it is the inertia of the body.