Question
Question: A 25watt, 220 volt bulb and 100 watt, 220 volt bulbs are connected in series across 440 volt lines. ...
A 25watt, 220 volt bulb and 100 watt, 220 volt bulbs are connected in series across 440 volt lines.
A) Only 100 watt bulb will fuse
B) Only 25 watt bulb will fuse
C) None of these bulbs will fuse
D) Both bulbs will fuse
Solution
In such types of questions first we calculate the resistance of the bulb and the maximum current which can flow from the bulb. If the current flown in the whole circuit is greater than the maximum current of the bulb in that condition the bulb will fuse.
Complete step-by-step answer:
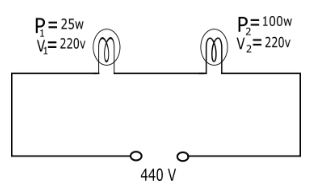
We have two bulb marked as P1=25w 220V and P2=100w 220V are connected in series with 440V source as given below
Step 1
First we calculate the resistance of both bulbs.
We know P=RV2 where P⇒ power of bulb which marked on bulb
V⇒ Voltage marked on bulb
R⇒ Resistance of bulb which always remain same
For bulb B1
P1=25w V1=220V
So P1=R1V12
Put value in this formula
⇒25=R12202
⇒25=R148400
⇒R1=2548400
By solving this
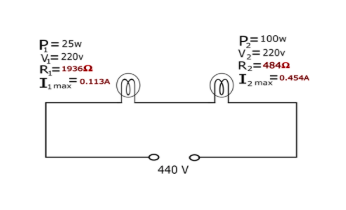
⇒R1=1936Ω
This is the resistance of Bulb 1
Now for second bulb
P2=100w V2=220V
Apply same method
P2=R2V22
⇒100=R12202
By solving this
⇒R2=10048400
⇒R2=484Ω
We get the resistance of both bulb is R1=1936Ω R2=484Ω
Step 2
In this step we calculate the maximum current which can flow from bulb 1 and bulb 2 without damaging them
Maximum current can flow from bulb can find with the help of formula P=V×I
Where P⇒ power of bulb
V⇒ Voltage of bulb which given on bulb
Apply this formula for both bulbs
For bulb B1
P1=V1×I1max
⇒25=220×I1max
⇒I1max=22025
By solving this
⇒I1max=0.113A
Now for B2
P2=V2×I2max
⇒100=220×I2max
⇒I1max=220100
By solving this
⇒I1max=0.454A
In this step we get the maximum current for both bulbs which can flow through bulb easily without damaging them
Step 3
In this step we will calculate the current flow from the whole circuit when bulbs connected in series with 440V supply
Resultant resistance of this circuit is R=R1+R2
⇒R=1936Ω+484Ω
⇒R=2420Ω
We know V=I×R
Where V⇒ voltage given in supply
Put the value and solving
⇒440=I×2420
⇒I=2420440
Further solving
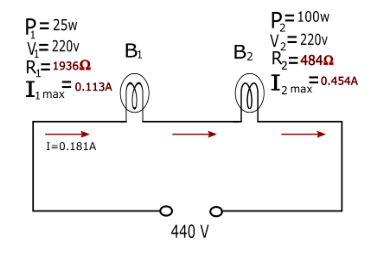
⇒I=0.181A
Step 4
Now we clearly see that the current flow by 440 V source is 0.181A
Which is exceeds the I1max=0.113A so the bulb 1 can not bear this much current so it will fuse but the I2max=0.454A is greater than current flow by supply so bulb 2 will not fuse.
Bulb 1 I1max<I⇒ fuse
Bulb 2 I2max>I⇒ not fuse
Hence in this question option B is correct.
Note: As we see if we want to solve such type of question then we have to find the current which a bulb can bear if the battery gives more current in the circuit if bulb connected in series the current in both bulb is same as current flowing in circuit than in that condition filament of bulb get heat and melt and finally that bulb will be fuse.
