Question

A point-like object of mass 2.0 kg moves along the x-axis with a velocity of +4.0 m/s. A net horizontal force acting along the x-axis is applied to the object with the force-time profile shown. What is the total work that was done by the force?

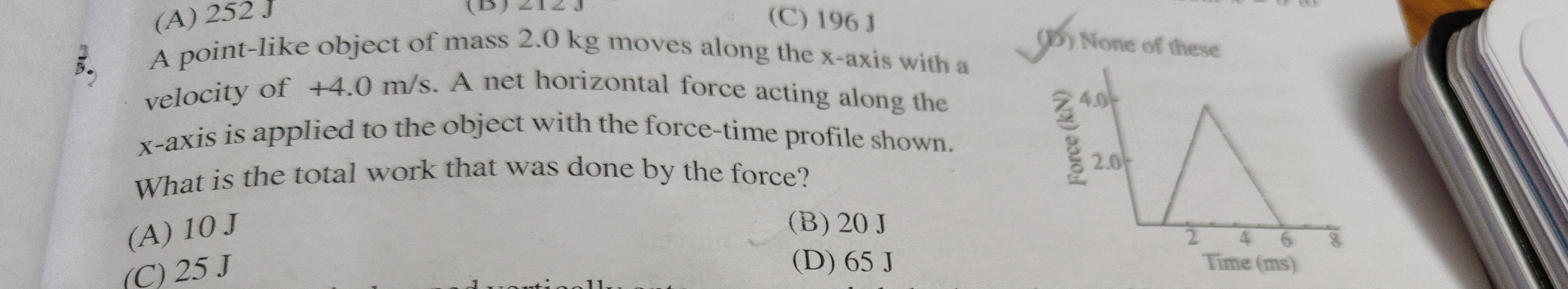
• A. 10 J
• B. 20 J
• C. 25 J
• D. 65 J

Answer 1

None of these

Answer 2

To find the total work done by the force, we will use the Work-Energy Theorem, which states that the total work done on an object is equal to the change in its kinetic energy.

$W = \Delta KE = \frac{1}{2}mv_f^2 - \frac{1}{2}mv_i^2$

First, we need to determine the final velocity ($v_f$) of the object. We can do this using the Impulse-Momentum Theorem, which states that the impulse (J) applied to an object is equal to the change in its momentum.

$J = \Delta p = mv_f - mv_i$

The impulse (J) is the area under the Force-Time (F-t) graph. The given graph is a triangle. The base of the triangle extends from $t = 0$ ms to $t = 6$ ms.

Base ($B$) = $6 \text{ ms} = 6 \times 10^{-3} \text{ s}$

The maximum height of the triangle (peak force) occurs at $t = 2$ ms and is $4.0 \text{ kN}$.

Height ($H$) = $4.0 \text{ kN} = 4.0 \times 10^3 \text{ N}$

1. Calculate the Impulse (J):

   The area of a triangle is $\frac{1}{2} \times \text{base} \times \text{height}$.

   $J = \frac{1}{2} \times B \times H$

   $J = \frac{1}{2} \times (6 \times 10^{-3} \text{ s}) \times (4.0 \times 10^3 \text{ N})$

   $J = \frac{1}{2} \times (6 \times 4.0) \times (10^{-3} \times 10^3) \text{ Ns}$

   $J = \frac{1}{2} \times 24 \times 1 \text{ Ns}$

   $J = 12 \text{ Ns}$

2. Calculate the Final Velocity ($v_f$):

   Given mass ($m$) = $2.0 \text{ kg}$

   Initial velocity ($v_i$) = $+4.0 \text{ m/s}$

   Using the Impulse-Momentum Theorem:

   $J = mv_f - mv_i$

   $12 \text{ Ns} = (2.0 \text{ kg}) v_f - (2.0 \text{ kg})(4.0 \text{ m/s})$

   $12 = 2v_f - 8$

   $2v_f = 12 + 8$

   $2v_f = 20$

   $v_f = 10 \text{ m/s}$

3. Calculate the Total Work Done (W):

   Using the Work-Energy Theorem:

   $W = \frac{1}{2}mv_f^2 - \frac{1}{2}mv_i^2$

   $W = \frac{1}{2}(2.0 \text{ kg})(10 \text{ m/s})^2 - \frac{1}{2}(2.0 \text{ kg})(4.0 \text{ m/s})^2$

   $W = (1.0)(100) - (1.0)(16)$

   $W = 100 - 16$

   $W = 84 \text{ J}$

The calculated total work done by the force is 84 J. Comparing this with the given options, none of the provided options match the calculated value of 84 J. Therefore, if "None of these" is an implied option, that would be the correct choice.