Question
Question: $|a| = \sqrt{3}, |b| = 5, c = 10$ and angle between $b$ and $c$ is $\frac{\pi}{3}$. If $a$ is perpen...
∣a∣=3,∣b∣=5,c=10 and angle between b and c is 3π. If a is perpendicular to b×c, then the value of ∣a×(b×c)∣ is
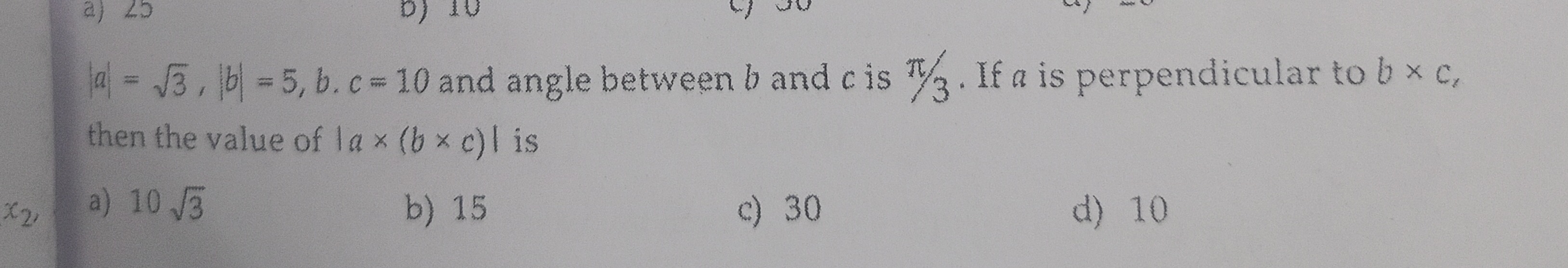
A
103
B
15
C
30
D
10
Answer
75
Explanation
Solution
We are given: ∣a∣=3,∣b∣=5,∣c∣=10, and the angle between b and c is 3π.
Also, since a⊥(b×c), it follows that the angle between a and (b×c) is 90∘. Hence,
∣a×(b×c)∣=∣a∣∣b×c∣(since sin90∘=1).
First, compute:
∣b×c∣=∣b∣∣c∣sin3π=5⋅10⋅23=50⋅23=253.
Thus,
∣a×(b×c)∣=3⋅253=25⋅3=75.
Therefore, the value of ∣a×(b×c)∣ is 75.
