Question
Question: $|a| = \sqrt{3}, |b| = 5, b.c = 10$ and angle between b and c is $\frac{\pi}{3}$. If a is perpendicu...
∣a∣=3,∣b∣=5,b.c=10 and angle between b and c is 3π. If a is perpendicular to b×c, then the value of ∣a×(b×c)∣ is
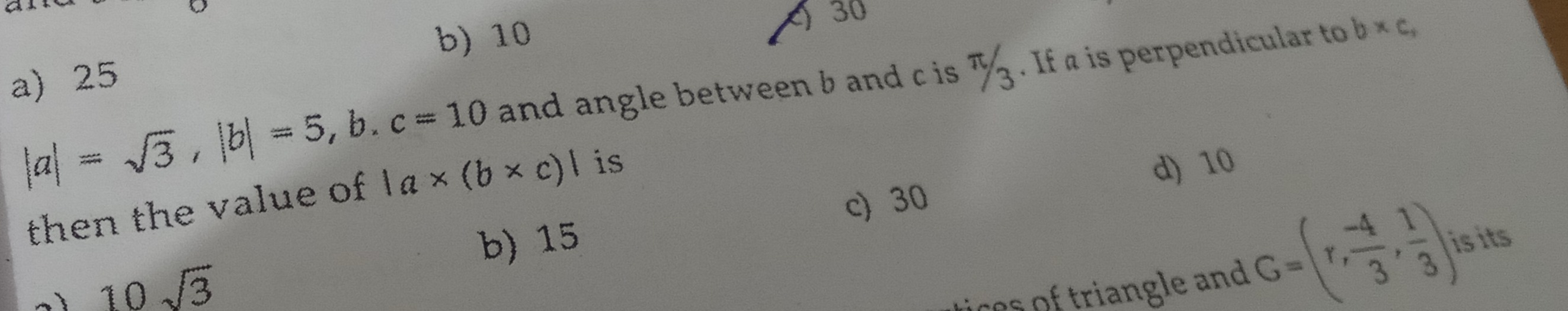
A
103
B
15
C
30
D
10
Answer
30
Explanation
Solution
Solution:
We are given:
- ∣a∣=3,∣b∣=5
- The dot product b⋅c=10
- The angle between b and c is 3π.
Since b⋅c=∣b∣∣c∣cos(3π), we have:
10=5⋅∣c∣⋅(21)
∣c∣=510×2=4
Compute ∣b×c∣ using:
∣b×c∣=∣b∣∣c∣sin(3π)=5⋅4⋅(23)=103
Given a⊥(b×c), we have:
∣a×(b×c)∣=∣a∣⋅∣b×c∣=3⋅103=30
Answer: Option (c) 30
