Question

A $24.5cm$ long string has a mass of $3.5g$ and a tension of $8.6kN$ . A standing wave of the ${{4}^{th}}$ harmonic is created on the string.
How many nodes are on this standing wave? How many wavelengths are on this standing wave? What is the speed of the wave on the string? What is the wavelength of this standing wave? What is the frequency of this standing wave?

Answer 1

In order to answer this question, we will study the different components of wave. We will also discuss the concept of standing waves or the reflection of waves from a surface.
The speed of a standing wave: $v=\sqrt{\dfrac{T}{\mu }}$
Where $T$ is the tension and $\mu$ is the linear density.
The frequency of the standing wave: $f=\dfrac{v}{\lambda }$
Where $v$ is the velocity and $\lambda$ is the wavelength.

Complete step by step answer:
We've been researching moving waves, or waves that move energy from one location to another. In some special cases, waves will bounce back and forth through a region under some circumstances, essentially becoming stationary. They are referred to as standing waves.
The wave shown below is a standing wave of ${{4}^{th}}$ harmonic created on a string which is $24.5cm$ long, having a mass of $3.5g$ and experiencing a tension force of $8.6kN$ .

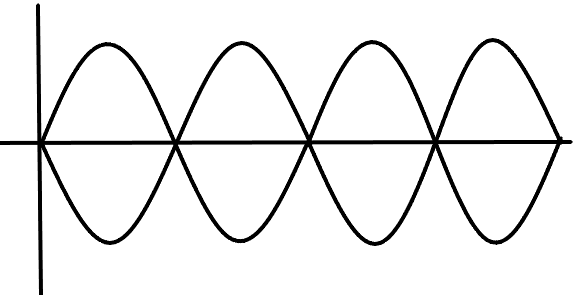
(a) A node is a point on a standing wave where the amplitude is the smallest. For example, the nodes at the ends of a vibrating guitar string. The guitarist adjusts the effective length of the vibrating string and hence the note played by adjusting the location of the end node by frets.

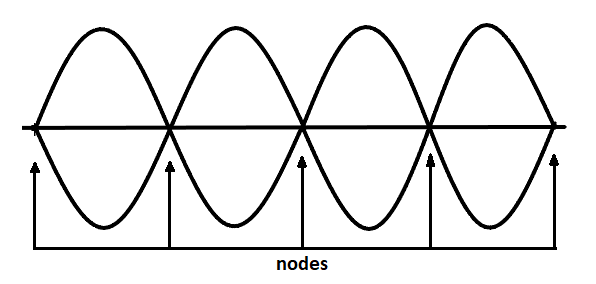
As seen in the above figure, a wave of ${{4}^{th}}$ harmonic consists of five nodes.
(b) The wavelength of a waveform signal propagated in space or along a string is the distance between similar points (adjacent crests) in adjacent cycles.

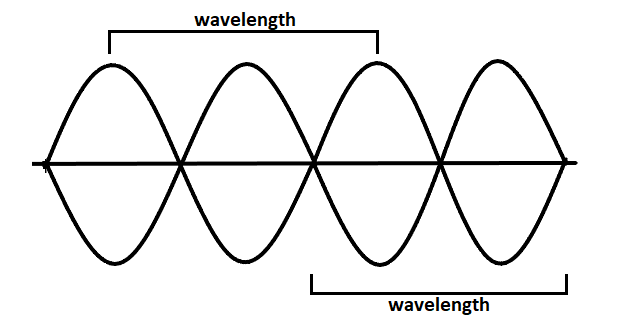
As we can see in the above figure, a wave of ${{4}^{th}}$ harmonic consists of two complete wavelengths.
(c) The square root of the tension divided by the mass per length, the linear density, determines the speed of a wave on a string. The equation that can be used to calculate the speed of a pulse or wave on a string under stress is given by:
$v=\sqrt{\dfrac{T}{\mu }}$
$\Rightarrow v=\sqrt{\dfrac{8.6\times {{10}^{+3}}N}{\dfrac{3.5g}{24.5cm}}}$
Where, $\left[ \mu =\dfrac{3.5g}{24.5cm} \right]$ is the linear density.
$\Rightarrow v=\sqrt{60200}$
$\Rightarrow v=245.4m{{s}^{-1}}$
Therefore, the speed of the standing wave is found to be $v=245.4m{{s}^{-1}}$ .
(d) As we already know that the standing wave consists of two complete wavelengths, therefore, the wavelength can be calculated as
$\begin{aligned} & 2\lambda =24.5cm \\\ & \Rightarrow \lambda =\dfrac{24.5}{2}cm \\\ & \Rightarrow \lambda =12.25cm \\\ \end{aligned}$
(e) Now, as we all know the relationship between the frequency, wavelength and velocity of the wave, we can calculate the frequency as
$\begin{aligned} & v=f\times \lambda \\\ & \Rightarrow f=\dfrac{v}{\lambda } \\\ & \Rightarrow f=\dfrac{245.4}{12.25} \\\ & \Rightarrow f=20Hz \\\ \end{aligned}$

Note:
It is very important to keep in mind that the wave we are discussing is of the ${{4}^{th}}$ harmonics. If the wave is of a different number of harmonics apart from four, then all the answers which we derived in the above example will have a different value. Apart from the values of mass, length and tension which will have similar effects, if changed.