Question

A $20kg$ metal block is placed on a horizontal surface. The block just begins to slide when a horizontal force of $100N$ is applied to it.

1. Calculate the coefficient of static friction.
2. If the coefficient of kinetic friction is $0.4$ then find the minimum force to maintain its uniform motion?

Answer 1

First of all the force given to us is the static force and now using the force of friction formula we can find the coefficient of static force and here the normal force acting on the block is equal to the weight of the block. Then for the second bit we have to use Newton's Second law of motion and from that we can find the minimum force to maintain the block in uniform motion.

Complete step by step answer:
As per the problem we have a $20kg$ metal block placed on a horizontal surface. The block just begins to slide when a horizontal force of $100N$ is applied to it.

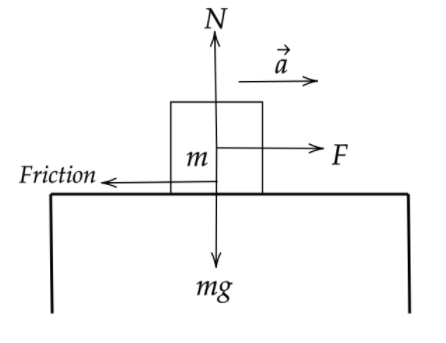
1. At the string we know that the $100N$ force is just enough to overcome static friction so we can write,
   Force = Static Friction
   We know the formula of static friction as,
   $F = {\mu _S}N \ldots \ldots \left( 1 \right)$
   Where,
   ${\mu _S}$ is the coefficient of static friction.
   $N$ is the normal reaction on the metal block.
   $F = 100N$ is the force acting on the body.
   Where the normal reaction in this kind of case is equal to the weight of the block.
   Hence we can write,
   $N = mg$
   Where $m = 20kg$ is the mass of the body and $g = 9.8m{s^{ - 1}}$ is the acceleration due to gravity.
   $N = 20 \times 9.8N = 196N$
   Now on putting all the known values in equation $\left( 1 \right)$we will get,
   $100N = {\mu _S} \times 196N$
   Rearranging the above equation we will get,
   ${\mu _S} = \dfrac{{100N}}{{196N}}$
   Hence the coefficient of static friction ${\mu _S} = 0.51$.
2. Now when the block starts moving the kinetic friction comes into play and to make the block move in uniform motion we need to equate the acceleration to zero so as to move in constant velocity.
   Now on using newton's second law of motion we will get,
   $\sum F = ma$
   Where,
   Summation of all the forces acting on the body is equal to the product of mass, $m$ with acceleration, $a$ of the body.
   Now in our case there are two forces one is the force due to motion of the body and the other one is the kinetic friction.
   Now on putting this force in equation$\left( 2 \right)$ we will get,
   $F - {F_{kinetic}} = ma$
   Where,
   Acceleration is equal to zero and kinetic friction is represented as ${F_{kinetic}} = {\mu _K}N$
   We know the value of the coefficient of kinetic friction ${\mu _K} = 0.4$.
   Now putting all the known values in the above equation we will get,
   $F - {\mu _K}N = 0$
   Rearranging the above equation we will get,
   $F = {\mu _K}N$
   Now putting the values of ${\mu _K}$ and N we will get,
   $F = 0.4 \times 196N = 78.4N$
   Hence the minimum force acting on the body to maintain its uniform motion is $78.4N$.

Note: In the above problem the normal reaction will remain the same for the body in both the cases, as the weight of the body never changes in any kind of motion. Remember that static friction is the friction which acts in between two or more solid objects that are not moving relative to each other while the kinetic friction is the force that acts in between two or more surfaces when the bodies are moving with some relative motion.