Question

A $20gm$ bullet moves with a velocity ${v_o}$ and pierces through a plate A of mass $1Kg$ and then comes to rest inside a second plate B of mass $2 \cdot 98Kg$ as in figure. It is found that the two plates initially at rest now move with equal velocity. What is the velocity of the bullet when it is between A and B.

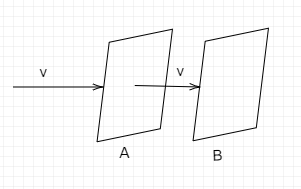
A. ${v_o}$
B. $\dfrac{{{v_o}}}{3}$
C. $\dfrac{{{v_o}}}{2}$
D. $\dfrac{{2{v_o}}}{3}$
E. $\dfrac{{3{v_o}}}{4}$

Answer 1

Linear momentum is the product of mass and velocity. Linear momentum in elastic collision is always constant and linear momentum is conserved always. The linear momentum is a vector quantity so it also depends upon the direction of the bodies after the collision.

Complete answer:
The initial velocity of the bullet is ${v_o}$ and the mass of the bullet is $20gm$ and in kilograms it will be $0 \cdot 02Kg$ also the mass of plate A is $1Kg$ and the mass of the plate B is$2 \cdot 98Kg$.
Apply the conservation of linear momentum when the bullet has pierced plate A and is in between plate A and B.
As the initial velocities of the plate A is zero and as the bullet pierced the plate A the velocity of plate A becomes V therefore,
$\Rightarrow {M_1}{v_o} = {M_1}v + {M_2}V$
$\Rightarrow \left( {0 \cdot 02} \right){v_o} = \left( {0 \cdot 02} \right)v + 1 \cdot V$………eq. (1)
Applying the conservation of linear momentum after the bullet hits plate B and they both move together with the same velocity with which the plate A is moving which is V.
$\Rightarrow {M_1}v = \left( {{M_1} + {M_3}} \right)V$
Where V is the velocities of both the plates
$\Rightarrow \left( {0 \cdot 02} \right)v = \left( {0 \cdot 02 + 2 \cdot 98} \right)V$
$\Rightarrow \left( {0 \cdot 02} \right)v = \left( 3 \right)V$
$\Rightarrow V = \left( {0 \cdot 02} \right) \cdot \dfrac{v}{3}$.........eq (2)
Replace the value of V from equation (2) in equation (1).
$\Rightarrow \left( {0 \cdot 02} \right){v_o} = \left( {0 \cdot 02} \right)v + 1 \cdot V$
$\Rightarrow \left( {0 \cdot 02} \right){v_o} = \left( {0 \cdot 02} \right)v + 1 \cdot \left( {0 \cdot 02} \right) \cdot \dfrac{v}{3}$
$\Rightarrow \left( {0 \cdot 02} \right){v_o} = \left( {0 \cdot 02} \right) \cdot \left( {v + \dfrac{v}{3}} \right)$
$\Rightarrow {v_o} = \left( {v + \dfrac{v}{3}} \right)$
$\Rightarrow {v_o} = \left( {\dfrac{{4v}}{3}} \right)$
$\Rightarrow v = \left( {\dfrac{{3{v_o}}}{4}} \right)$
So the velocity of the bullet when it is between plates A and B is $v = \left( {\dfrac{{3{v_o}}}{4}} \right)$.

So the correct answer for this problem is option E.

Note:
The total momentum of a system is always constant in a closed system. The formula of the momentum is important and should be remembered as it helps to solve these kinds of problems also the linear momentum depends upon the direction of motion.