Question

A 20 V battery of internal resistance $1\Omega$ is connected to three coils of $12\Omega ,6\Omega ,\,\,{\text{and }}4\Omega$in parallel, a resistor of $5\Omega$ and a reversed battery (EMF 8 V and internal resistance$2\Omega$) as shown in fig. Calculate

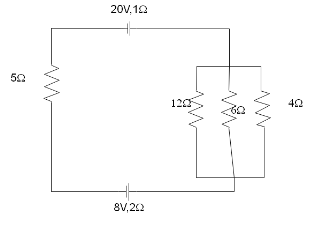
a. the current in the circuit,
b. current in the resistor of 12Ω coil, and
c. the potential difference across each battery.

Answer 1

Hint In this solution, we will calculate the net resistance of the circuit and the net EMF. We will then use ohm’s law to determine the current flowing in the circuit and hence the potential difference across each battery.
In this solution we will be using the following formula
Ohm’s law: $V = IR$ where $V$ is the potential of the battery, $I$ is the current in the circuit which has a net resistance $R$.

Complete step by step answer
In the circuit given to us, the two batteries are connected such that their positive and negative ends are attached. In this configuration, the two batteries oppose each other and the net EMF is the difference between the two batteries which we can calculate as
$\Rightarrow V = 20 - 8$
$\Rightarrow V = 12\,V$
Let us now calculate the net resistance of the circuit. The combined resistance of the three resistors in parallel can be calculated as
$\Rightarrow \dfrac{1}{R} = \dfrac{1}{{12}} + \dfrac{1}{6} + \dfrac{1}{4}$
Taking the LCM on the right side, we get
$\Rightarrow \dfrac{1}{R} = \dfrac{6}{{12}}$
$\Rightarrow R = 2\,\Omega$
The set of parallel resistors is in series with the other resistors of $5\,\Omega$ and the internal resistances of the battery. The net resistance of the circuit can hence be calculated as:
$\Rightarrow {R_{net}} = 2 + 5 + 1 + 2$
$\Rightarrow {R_{net}} = 10\,\Omega$
Then using ohm’s law, we can calculate the current flowing in the circuit as
$\Rightarrow I = \dfrac{V}{{{R_{net}}}}$
Substituting $V = 12$ , we get
$\Rightarrow I = \dfrac{{12}}{{10}}$ which is the answer to question (a)
$\Rightarrow I = 1.2\,A$
We can now calculate the current flowing through the resistor $12\,\Omega$ .
As the current in a parallel circuit splits in the inverse ratio of the resistors in the branches, we can find the current in the $12\,\Omega$ as
${I_{12}} = \dfrac{R}{{12}} \times I$ which is the answer to question (b)
$\Rightarrow {I_{12}} = \dfrac{2}{{12}} \times 1.2 = 0.2\,A$
The potential difference across each battery will be due to the EMF of the battery and the drop in voltage due to the internal resistance of the battery.
Thus the potential difference across the 20 V battery will be
${V_{20}} = 20 - I{r_{int}}$ where ${r_{int}}$ is its internal resistance. On substituting $I = 1.2$, we get
$\Rightarrow {V_{12}} = 20 - (1.2 \times 1)$
Which gives us,
$\Rightarrow {V_{12}} = 18.8\,V$
For the 8 V battery, since the current would be flowing in the opposite direction wrt the potential of the battery, we have
${V_8} = 8 - ( - I){r_{int}}$
By substituting the values,
$\Rightarrow {V_8} = 8 + (1.2 \times 2)$
$\Rightarrow {V_8} = 5.6V$
Thus we have also found out the potential difference across the batteries.

Note
Since we have been given two batteries that oppose each other and have unequal voltages, one of them must overpower the other and as a result, the flow of current will be in the opposite direction for the battery with lower EMF which in this case was the 8 V battery. As a result, the current in the cell must be taken as negative of the actual current.