Question

A 2 MeV proton is moving perpendicular to a uniform magnetic field of 2.5 tesla.
The force on the proton is
(A) $9.6 \times {10^{15}}N$
(B) $7.6 \times {10^{ - 12}}N$
(C) $9.6 \times {10^{12}}N$
(D) $7.6 \times {10^{12}}N$

Answer 1

To calculate the force on any moving charge particle we use following formula
$\vec F = q(\vec V \times \vec B)$
Where q $=$ Charge of particle
V $=$ Velocity of particle
B $=$ Magnetic field
$\boxed{F = qVB\sin \theta }$
Here $\theta$ is the angle between V & B

Complete step by step solution:
For calculating the magnetic force on protons first we have to analyze motion of the proton with respect to direction of magnetic field.

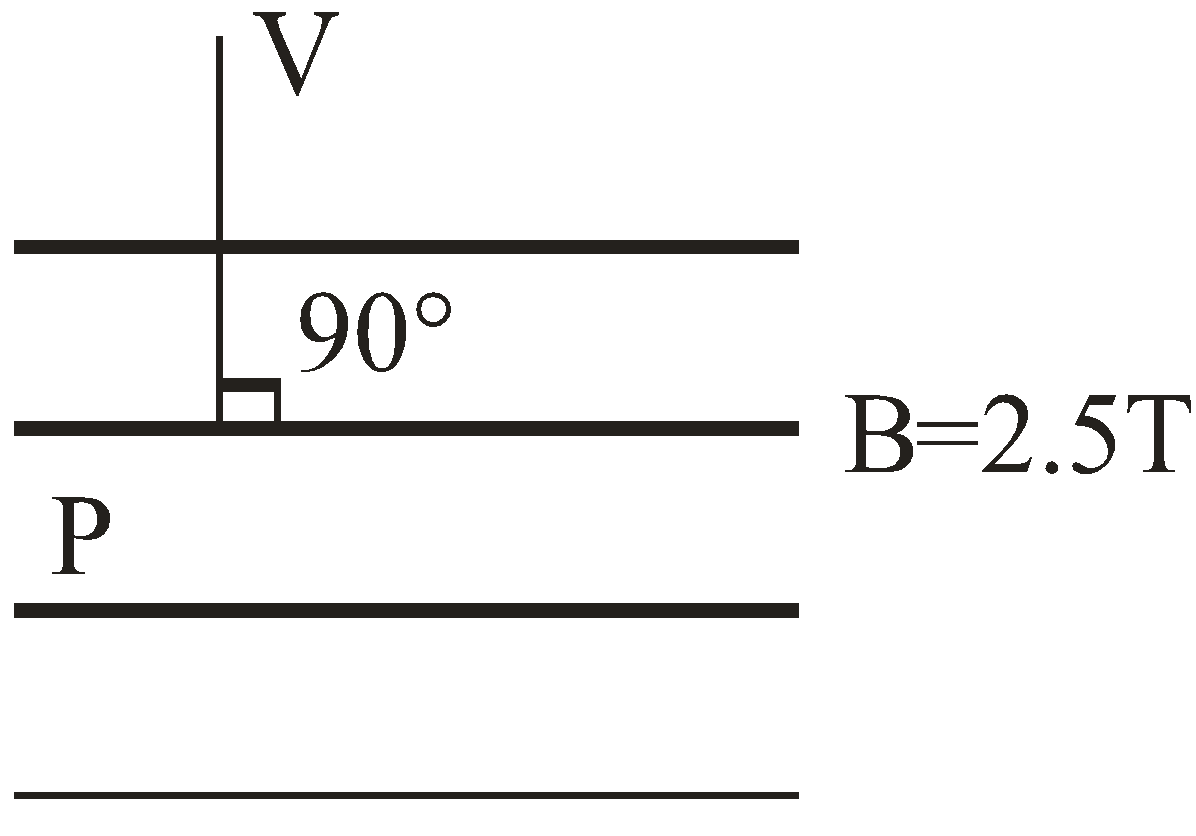
Here given that kinetic charge of proton is 2 MeV
i.e., $K.E = \dfrac{1}{2}m{V^2}$
$\dfrac{1}{2}m{V^2} = 2MeV = 2 \times {10^6} \times 1.6 \times {10^{ - 19}}$
Here m $=$ mass of proton $= 1.67 \times {10^{ - 27}}kg$
${V^2} = \dfrac{{2 \times 2 \times {{10}^6} \times 1.6 \times {{10}^{ - 19}}}}{{1.67 \times {{10}^{ - 27}}}}$
${V^2} = \dfrac{{4 \times {{10}^{ - 13}} \times {{10}^{27}} \times 1.6}}{{1.67}}$
${V^2} = 3.832 \times {10^{14}}$
$\boxed{V = 1.957 \times {{10}^7}m/s}$
We know that $\vec F = q(\vec V \times \vec B)$
$F = qVB\sin \theta$
Given that angle between V & B is $90^\circ$
So, $F = qVB\sin 90^\circ$
$F = qVB$
Given $q = 1.6 \times {10^{ - 19}}C,B = 2.5T$
$F = 1.6 \times {10^{ - 19}} \times 1.957 \times {10^7} \times 2.5$
$F \simeq 7.83 \times {10^{ - 12}}N$

So, option B is correct answer.

Note: In order to solve this type of problems first we have to convert the kinetic charge from MeV.
Where $1MeV = 1 \times {10^6} \times 1.6 \times {10^{ - 19}}J$