Question

A 2 kg block slides on a horizontal floor with a speed of $4m{{s}^{-1}}$. It strikes an uncompressed spring and compresses it till the block is motionless. The kinetic friction force is 15 N and the spring constant is $10000N{{m}^{-1}}$. The spring compresses by what amount?

Answer 1

We need to find the relation between a moving mass that collides with a spring and the impact caused by this collision. The impact is to be considered as the force which causes the spring to compress and thus, we can solve this problem.

Complete answer:
We are given a block of mass that slides and collides with a spring. The spring is compressed by this action until the block comes to rest. We can understand from this statement that the complete momentum from the block has been transferred to the spring. Also, there is the frictional force which is acting on the block. So, the complete kinetic energy of the block is converted to potential energy and frictional energy.

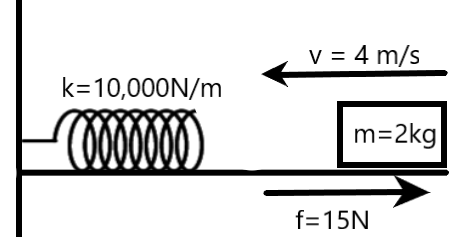
Now, the potential energy possessed by a compressed spring of spring constant k is given as –
$PE=\dfrac{1}{2}k{{x}^{2}}$
Where x is the compression caused in the spring.
Now, the kinetic energy is converted to potential energy and frictional energy as –

& KE=PE+{{E}_{f}} \\\ & \Rightarrow \dfrac{1}{2}m{{v}^{2}}=\dfrac{1}{2}k{{x}^{2}}+fx \\\ & \Rightarrow \dfrac{1}{2}(2){{(4)}^{2}}=\dfrac{1}{2}(10,000){{x}^{2}}+15x \\\ & \Rightarrow 10,000{{x}^{2}}+30x-32=0 \\\ \end{aligned}$$ $$\begin{aligned} & x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} \\\ & \Rightarrow x=\dfrac{-30\pm \sqrt{{{30}^{2}}-4(10000)(-32)}}{2(10000)} \\\ & \therefore x=0.0566m \\\ \end{aligned}$$ So, the length to which the spring compressed due to this block of mass colliding with it is almost 5.66cm. The spring has a relatively high spring constant which makes the compression harder for the block. This is the required solution. **Note:** We can see from the problem that the work done by a mass on a spring is stored in the spring as the potential energy which is later used to expand the spring back to its normal position and extend to the other end. Thus, the spring can oscillate itself.