Question

A $2\,kg$ block is placed over a $4\,kg$ block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is $0.20$ . The acceleration of the two blocks if a horizontal force of $12\,N$ is applied to the upper block $(g = 10m{s^{ - 2}})$
A. $4\,m{s^{ - 2}},2\,m{s^{ - 2}}$
B. $2\,m{s^{ - 2}},2\,m{s^{ - 2}}$
C. $3\,m{s^{ - 2}},3\,m{s^{ - 2}}$
D. $4\,m{s^{ - 2}},1\,m{s^{ - 2}}$

Answer 1

In this type of question first we will draw the figure and mention all the forces acting on it and after resolving all the forces according to the question we can easily get the answer.
Here we have drawn all the forces and then using Newton's law of motion we have solved the equation for acceleration.

Formula used:
$f = ma$
Where, $f$ is the force, $m$ is the mass and $a$ is the acceleration.

Complete step by step answer:

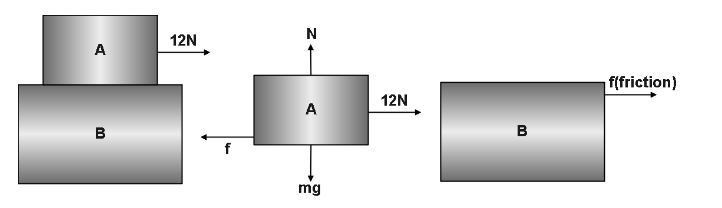
At first let us consider block A, from Newton’s law of motion, we can say that,
$f = ma$
$\Rightarrow 12 - f = {m_A}a$ -----(1)
And now let us consider block B,
From Newton’s law of motion, we can say that,
$f = ma$
$\Rightarrow f = {m_B}a$ -----(2)
Now, adding equation (1) and (2)
$12 = ({m_A} + {m_B})a$
Now, substituting the values to find out the acceleration,
$12 = ({m_A} + {m_B})a \\\ \Rightarrow 12 = 6a \\\ \Rightarrow a = 2m{s^{ - 2}} \\\$
Now, putting the value of $a$ in equation (2)
$f = {m_B}a \\\ \Rightarrow f = 4 \times 2 \\\ \Rightarrow f = 8N \\\$
But we know that ${f_{\max }} = \mu \times {\rm N}$
Therefore, we can say that to move together without slipping, friction force required is $8N$ but maximum value of friction is $4N$. Therefore, our assumption is wrong that they will slip and,
$f = {f_{\max }} = 4N$
Therefore, for block A,
$12 - f = \dfrac{{{m_A}a}}{{{a_A}}}$
Now, substituting all the value,
$12 - f = \dfrac{{{m_A}a}}{{{a_A}}} \\\ \Rightarrow 12 - 4 = 2{a_A} \\\ \Rightarrow 8 = 2{a_A} \\\ \Rightarrow {a_A} = 4m{s^{ - 2}} \\\$
Similarly for block B,
$f = {m_B}{a_B} \\\ \Rightarrow 4 = 4{a_B} \\\ \therefore {a_B} = 1m{s^{ - 2}}$
So, the acceleration of block A is $4\,m{s^{ - 2}}$ and block B is $1\,m{s^{ - 2}}$ .

Hence the correct option is D.

Note: Check if sliding is happening or not. Assume sliding is not happening and they are moving with an acceleration of $a$. Remember if ${f_{\max }} < f$ then the block will move with different acceleration in this case apply friction and calculate the acceleration.