Question

A 2 kg block A is attached to one end of a light string that passes over an ideal pulley and a 1 kg sleeve B slides down the other part of the string with an acceleration of 5 m/s² with respect to the string. Find the acceleration of the block, acceleration of sleeve and tension in the string. [g = 10 m/s²]

Answer 1

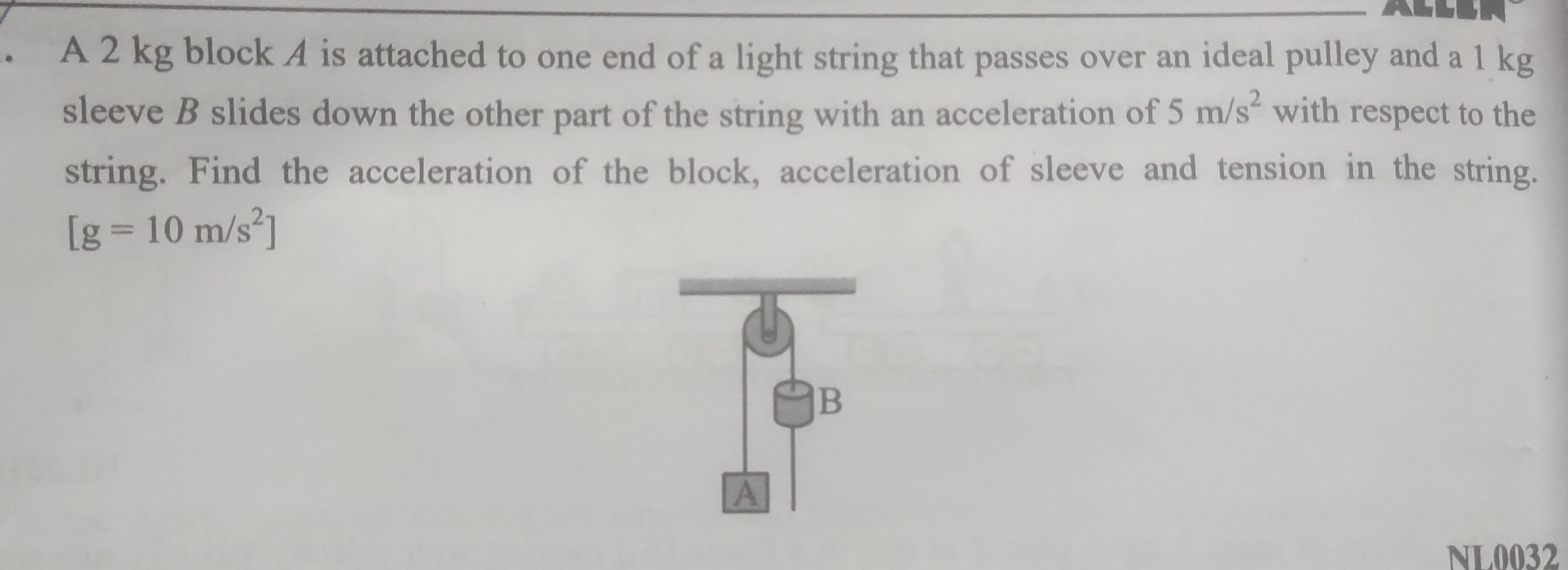
Acceleration of block = 5 m/s² downwards, Acceleration of sleeve = 0 m/s², Tension in string = 10 N

Answer 2

The problem involves a block, a sleeve, an ideal pulley, and a string. We need to apply Newton's second law and the concept of relative acceleration.

Given:

• Mass of block A, $m_A = 2$ kg
• Mass of sleeve B, $m_B = 1$ kg
• Acceleration of sleeve B with respect to the string, $a_{B,S} = 5 \, \text{m/s}^2$ (downwards along the string)
• Acceleration due to gravity, $g = 10 \, \text{m/s}^2$

1. Define Accelerations and Directions:

Let $a_A$ be the magnitude of the acceleration of block A.
Let $a_B$ be the magnitude of the absolute acceleration of sleeve B (relative to the ground).
Let's assume block A moves downwards. Therefore, the string on A's side moves downwards with acceleration $a_A$. Consequently, the string on B's side moves upwards with acceleration $a_A$.

2. Relative Acceleration Relationship:

The absolute acceleration of sleeve B ($a_B$) is the vector sum of its acceleration relative to the string ($a_{B,S}$) and the acceleration of the string relative to the ground ($a_{S,G}$).
Since $a_{B,S}$ is downwards (5 m/s²) and the string on B's side is moving upwards with $a_A$, we can write:
$a_B = a_{B,S} - a_A$ (taking downwards as positive for sleeve B)
$a_B = 5 - a_A$ (Equation 1)

3. Free Body Diagrams and Equations of Motion:

• For Block A:
  Forces acting on block A:

  • Weight $m_A g$ acting downwards.
  • Tension $T$ acting upwards.
    Assuming A moves downwards, apply Newton's second law ($F_{net} = ma$):
    $m_A g - T = m_A a_A$
    $2(10) - T = 2 a_A$
    $20 - T = 2 a_A$ (Equation 2)

• For Sleeve B:
  Forces acting on sleeve B:

  • Weight $m_B g$ acting downwards.
  • Tension $T$ acting upwards (from the string passing through it).
    Assuming B moves downwards (which is consistent with $a_{B,S}$ being downwards), apply Newton's second law:
    $m_B g - T = m_B a_B$
    $1(10) - T = 1 a_B$
    $10 - T = a_B$ (Equation 3)

4. Solve the System of Equations:

Substitute Equation 1 into Equation 3:
$10 - T = (5 - a_A)$
From this, we can express $T$:
$T = 10 - (5 - a_A)$
$T = 5 + a_A$ (Equation 4)

Now substitute Equation 4 into Equation 2:
$20 - (5 + a_A) = 2 a_A$
$15 - a_A = 2 a_A$
$15 = 3 a_A$
$a_A = \frac{15}{3}$
$a_A = 5 \, \text{m/s}^2$

Since $a_A$ is positive, our initial assumption that block A moves downwards is correct.

5. Calculate Tension and Acceleration of Sleeve B:

• Acceleration of the block (A):
  $a_A = 5 \, \text{m/s}^2$ (downwards)

• Tension in the string (T):
  Substitute $a_A = 5 \, \text{m/s}^2$ into Equation 4:
  $T = 5 + 5$
  $T = 10 \, \text{N}$

• Acceleration of the sleeve (B):
  Substitute $a_A = 5 \, \text{m/s}^2$ into Equation 1:
  $a_B = 5 - a_A$
  $a_B = 5 - 5$
  $a_B = 0 \, \text{m/s}^2$

This means sleeve B remains stationary relative to the ground while sliding down the string.