Question
Question: A circle of radius 'r' passes through both foci and exactly four points on the ellipse with equation...
A circle of radius 'r' passes through both foci and exactly four points on the ellipse with equation x2+16y2=16. The set of all possible values of r is an interval [a,b), then a + b is equal to -
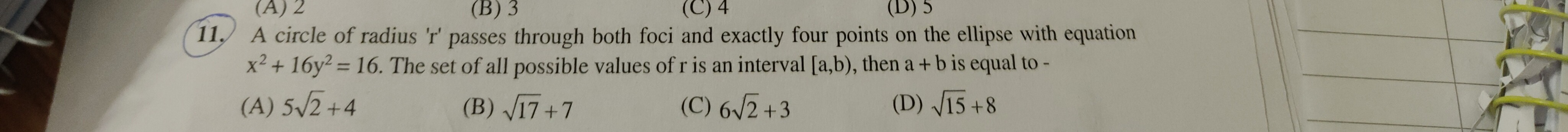
(A) 52+4
(B) 17+7
(C) 62+3
(D) 15+8
15+8
Solution
The ellipse equation is 16x2+1y2=1. Here, a=4 and b=1. The distance from the center to the foci is c=a2−b2=16−1=15. The foci are at (±15,0).
Let the circle have radius r and center (0,k) (since it passes through both foci, its center lies on the y-axis). The distance from (0,k) to (15,0) is r, so r2=(15−0)2+(0−k)2=15+k2.
The equation of the circle is x2+(y−k)2=r2. Substituting x2=16(1−y2) from the ellipse equation: 16(1−y2)+(y−k)2=r2 16−16y2+y2−2ky+k2=15+k2 −15y2−2ky+1=0 15y2+2ky−1=0
For exactly four intersection points, the quadratic equation for y must have two distinct real roots, y1 and y2, such that −1<y1<1 and −1<y2<1. This requires:
- Discriminant Δ>0: (2k)2−4(15)(−1)=4k2+60>0 (always true).
- f(1)>0 and f(−1)>0, where f(y)=15y2+2ky−1. f(1)=15+2k−1=14+2k>0⟹k>−7. f(−1)=15−2k−1=14−2k>0⟹k<7. So, −7<k<7.
The radius squared is r2=15+k2. Since −7<k<7, we have 0≤k2<49. Therefore, 15≤r2<15+49, which means 15≤r2<64. Taking the square root (and since r>0), we get 15≤r<8. The interval is [a,b)=[15,8). So, a=15 and b=8. a+b=15+8.
