Solveeit Logo
Login

Question

Question: A = (2, 4, 5) and B = (3, 5, -4) are two points. If the XY-plane, YZ-plane divide AB in the ratio a ...

A = (2, 4, 5) and B = (3, 5, -4) are two points. If the XY-plane, YZ-plane divide AB in the ratio a : b and p : q respectively, then ab+pq=\dfrac{a}{b}+\dfrac{p}{q}=
A. 2312\dfrac{23}{12}
B. −712\dfrac{-7}{12}
C. 712\dfrac{7}{12}
D. −2215\dfrac{-22}{15}

Explanation

Solution

The line AB is divided internally by XY-plane and YZ-plane. So, we will use the section formula internally to solve this question, that is (mx2+nx1m+n,my2+ny1m+n,mz2+nz1m+n)\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n},\dfrac{m{{z}_{2}}+n{{z}_{1}}}{m+n} \right). The z coordinate of the XY-plane is zero and the x coordinate of the YZ-plane is zero.

Complete step by step answer:
We will understand this question by first drawing the figure for the XY-plane as given below.

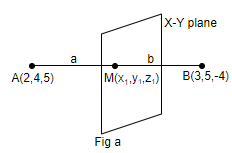
We can see in the above figure that M(x1,y1,z1)M\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right) is a point on XY-plane such that AB is divided internally by XY-plane in the ratio of a : b. So, we will now use the section formula internally to find the coordinate of M. We know that the section formula (internally) is given by the formula, (mx2+nx1m+n,my2+ny1m+n,mz2+nz1m+n)\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n},\dfrac{m{{z}_{2}}+n{{z}_{1}}}{m+n} \right). So, applying this, we have the coordinates of M(x1,y1,z1)M\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)as,
=(3a+2ba+b,5a+4ba+b,−4a+5ba+b)=\left( \dfrac{3a+2b}{a+b},\dfrac{5a+4b}{a+b},\dfrac{-4a+5b}{a+b} \right)
As we know that the z coordinate of XY-plane is equal to 0, therefore, we have,
z1=0 ⇒−4a+5ba+b=0 ⇒−4a+5b=0×(a+b) ⇒−4a+5b=0 ⇒4a=5b ⇒ab=54 \begin{aligned} & {{z}_{1}}=0 \\\ & \Rightarrow \dfrac{-4a+5b}{a+b}=0 \\\ & \Rightarrow -4a+5b=0\times \left( a+b \right) \\\ & \Rightarrow -4a+5b=0 \\\ & \Rightarrow 4a=5b \\\ & \Rightarrow \dfrac{a}{b}=\dfrac{5}{4} \\\ \end{aligned}
Now, we will draw the figure for the YZ-plane.

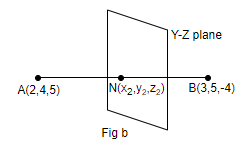
We can see form the above figure that N(x2,y2,z2)N\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) is a point on YZ-plane such that AB is divided internally by YZ-plane in the ratio of p : q. Now, we will again use the section formula internally to find the coordinate of N. So, applying the section formula (internally), we will have the coordinate of N(x2,y2,z2)N\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) as,
=(3p+2qp+q,5p+4qp+q,−4p+5qp+q)=\left( \dfrac{3p+2q}{p+q},\dfrac{5p+4q}{p+q},\dfrac{-4p+5q}{p+q} \right)
Now, we know that the x coordinate of YZ plane is equal to 0, therefore, we get,
x2=0 ⇒3p+2qp+q=0 ⇒3p+2q=0(p+q) ⇒3p+2q=0 ⇒3p=−2q ⇒pq=−23 \begin{aligned} & {{x}_{2}}=0 \\\ & \Rightarrow \dfrac{3p+2q}{p+q}=0 \\\ & \Rightarrow 3p+2q=0\left( p+q \right) \\\ & \Rightarrow 3p+2q=0 \\\ & \Rightarrow 3p=-2q \\\ & \Rightarrow \dfrac{p}{q}=\dfrac{-2}{3} \\\ \end{aligned}
We have obtained ab=54\dfrac{a}{b}=\dfrac{5}{4} and pq=−23\dfrac{p}{q}=\dfrac{-2}{3}, we can find ab+pq\dfrac{a}{b}+\dfrac{p}{q}. So, solving it we get,
54+(−23)⇒54−23⇒15−812=712\dfrac{5}{4}+\left( \dfrac{-2}{3} \right)\Rightarrow \dfrac{5}{4}-\dfrac{2}{3}\Rightarrow \dfrac{15-8}{12}=\dfrac{7}{12}
Thus, we get the value as, ab+pq=712\dfrac{a}{b}+\dfrac{p}{q}=\dfrac{7}{12}.

So, the correct answer is “Option C”.

Note: The students must remember that when a point lies somewhere between the two points, the line segment is divided internally. And when a point lies on the external part of the segment, that is when you extend the segment, then its actual length, the point lies there, then the line segment is divided externally. We have to use the section formulas for internal division as, (mx2+nx1m+n,my2+ny1m+n)\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right) and for external division as, (mx2−nx1m−n,my2−ny1m−n)\left( \dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n} \right).