Question

A $2.0cm$ tall object is placed perpendicular to the principal axis of a concave lens of focal length $15cm$. At what distance from the lens, should the object be placed so that it forms an image $10cm$ from the lens? Also find the nature and size of the image formed.

Answer 1

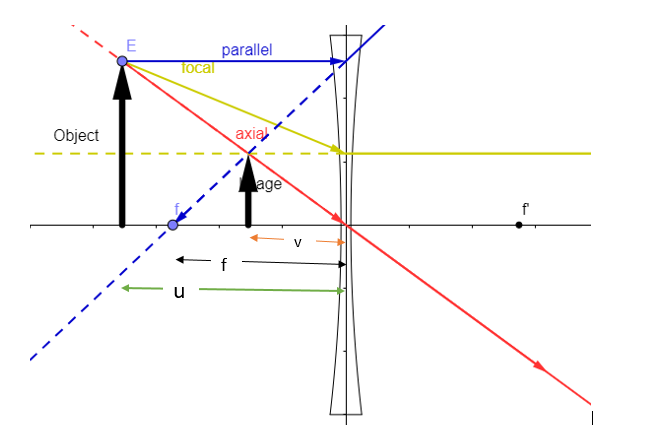
A concave lens always produces a virtual erect image of the object. Also the image is at the same side of the object. Take sign convention and write down all the values given. Then use the lens formula to calculate the object distance from the image distance and focal length. After finding the object distance calculate the magnification produced by the lens and equate the magnification with the ratio of image height to object height to get the image height. From the magnification value you can determine the nature of image.

Formula used:
Lens formula is given by
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$ .Where,
$\begin{aligned} & u=\text{ object distance from the lens} \\\ & v=\text{ image distance from the lens} \\\ & f=\text{focal length of the lens} \\\ \end{aligned}$
Magnification of lens,$m=\dfrac{h'}{h}=\dfrac{v}{u}$.where,
$\begin{aligned} & h'=\text{image height} \\\ & h=\text{object height} \\\ \end{aligned}$

Complete answer:

Given that
Height of image, $h=+2.0cm$
Focal length, $f=-10cm$ (because by sign convention the focal length of concave lens is taken to be negative)
Image distance, $v=-15cm$(because for concave lens the image is formed at left side of the lens so by sign convention the image distance will be negative)
Object distance. $u=?$

Using the lens equation we get
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
Putting the values of $f=-10cm$,$v=-15cm$we get
$\begin{aligned} & \dfrac{1}{-10}-\dfrac{1}{u}=\dfrac{1}{-15} \\\ &\Rightarrow\dfrac{1}{u}=\dfrac{1}{-10}-\left(\dfrac{1}{-15}\right)=\dfrac{1}{-10}+\dfrac{1}{15}=\dfrac{-3+2}{30}=\dfrac{-1}{30} \\\ & \Rightarrow \dfrac{1}{u}=-\dfrac{1}{30} \\\ & \Rightarrow u=-30cm \\\ \end{aligned}$

Thus the object is situated at a distance $30cm$ to the left of the mirror.
Now magnification of the lens is given by the ratio of image height to the object height. Also magnification is the ratio of image distance from the lens to the object distance from the lens. So

$\begin{aligned} & m=\dfrac{h'}{h}=\dfrac{v}{u} \\\ & \implies m=\dfrac{-10}{-30}=\dfrac{1}{3}=+0.33 \\\ \end{aligned}$

The positive sign of magnification indicates that the image is virtual erect. And the image is one-third the size of the object.
So the image is virtual, erect and diminished.

Note:
For problems involving lens and mirror the sign convention is the most important. By sign convention the object distance is always taken to be negative. If the value of magnification is negative then the nature of the image is real and inverted, and if the magnification is positive then the nature of image is virtual & erect.