Question

A 2.0 cm tall object is placed 15cm in front of a concave mirror of focal length 10cm. What is the size and nature of the image?
A. 4cm, real
B. 4cm, virtual
C. 1cm, real
D. none of these

Answer 1

Find the position of the image with the help of the mirror formula. They use the formula for magnification in terms of v and u and calculate the magnification. Then use the magnification formula in the term of heights of the image and the object to find the height of the image.

Formula used: $\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$
$m=-\dfrac{v}{u}$
$m=\dfrac{h'}{h}$

Complete step by step answer:
Complete step by step answer:
It is given that an object is placed in front of a concave mirror. When the light rays from a point of the object fall on the mirror, the light rays will reflect and intersect at a point. This point will be the position of the image of the object.

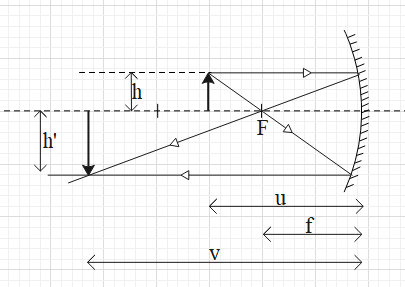
Now to calculate the size of the image we will use the formula for the magnification due to a spherical mirror. i.e. $m=\dfrac{h'}{h}$ ….. (i),
where h’ and h are the heights of the image and the object, according to the sign convection.
The magnification is also given as $m=-\dfrac{v}{u}$ …… (ii).
Here, v and u are the positions of the image and the object according to the sign convection.
If the magnification is negative, then the image will be a real image.
If the magnification is positive, then the image will be a virtual image.
We know that value of u (i.e. u = -15cm). So we have to find the value of v.
For this, we will use the mirror formula $\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$ ….. (iii).
f is the focal length of the mirror. For a concave mirror, f is always negative.
Here, u = -15cm, f = -10cm and h = 2cm.
Substitute the values of u and f in equation (iii).
$\Rightarrow \dfrac{1}{-10}=\dfrac{1}{v}+\dfrac{1}{-15}$
$\Rightarrow \dfrac{1}{v}=-\dfrac{1}{10}+\dfrac{1}{15}$
$\Rightarrow \dfrac{1}{v}=\dfrac{-3+2}{30}=\dfrac{-1}{30}$
$\Rightarrow v=-30cm$.
Substitute the value of u and v in equation (ii).
$\Rightarrow m=-\dfrac{(-30)}{(-15)}=-2$
Substitute the value of m and h in equation (i).
$\Rightarrow -2=\dfrac{h'}{2}$
$\Rightarrow h'=-4cm$
Therefore, the size of the image is 4cm and since the magnification is negative, the image formed is a real image.

So, the correct answer is “Option A”.

Note: A real image formed is always inverted. This means the magnification for a real image is always negative.
Therefore, if the magnification is negative, the image formed is a real image.
Also, note that the formula that we used above is applicable only when the aperture of the mirror is very large compared to the focal length of the mirror.