Question

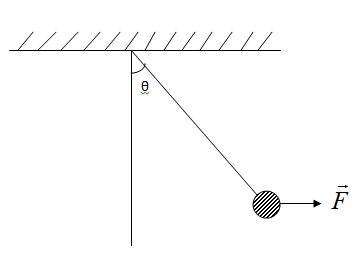
A 1N pendulum bob is held at an angle $\theta$ from the vertical by a 2N horizontal force $\vec{F}$ as shown in the figure. The tension in the string supporting the pendulum bob (in N) is:

& \text{A}\text{. }\cos \theta \\\ & \text{B}\text{. }\dfrac{2}{\cos \theta } \\\ & \text{C}\text{. }\sqrt{5} \\\ & \text{D}\text{. 1} \\\ \end{aligned}$$

Answer 1

Hint: In these types of questions, always try to find out all types of forces acting on that object. After that, equate the balancing horizontal as well as vertical forces, we get two questions. Then solving both equations, we find the required solution.

Complete step-by-step answer:
Let O be the point of rigid suspension.
Given that, the pendulum with bob having weight 1N is held at an angle $\theta$ from the vertical.
There is a horizontal force $\vec{F}$ of 2N acting on a bob.

We will first find out the all forces acting on the bob. The basic and important force is the gravitational force acting on the bob which is 1N and horizontal force 2N.

Let us consider To be the tension in the string of the pendulum which is along the string towards the suspension point O. Now, we resolve the tension T into two components, $T\sin \theta$in horizontal direction and $T\cos \theta$ in upward direction.

Equating balancing horizontal forces, we get

$\vec{F}=T\sin \theta$ i.e. $2N=T\sin \theta$ …..(1)
And balancing vertical forces,

$T\cos \theta =mg$ i.e. $T\cos \theta =1N$ …..(2)

Dividing equations (1) by (2), we get,

$\tan \theta =2$
$\theta ={{\tan }^{-1}}2$
$\theta ={{63.4349}^{0}}$
Using this value in equation (2) we get,
$T\cos \left( 63.4349 \right)=1N$
$T=2.236N$
$T=\sqrt{5}N$

Hence, the tension in the string supporting the pendulum bob is $\sqrt{5}N$.
Correct option is C.

Note: When we multiply mass by acceleration due to gravity, then it is known as ‘weight’ and it has a unit of Newton: $\text{Weight}=\text{mass}\times g$, here g is acceleration due to gravity. Students should know how to resolve vectors in two components because it is very necessary in physics for problem solving.