Question

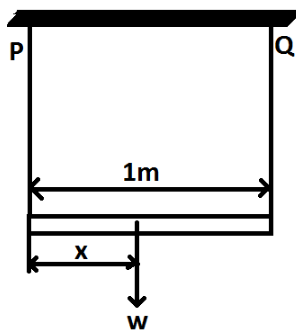
A $1m$ long rod of negligible weight is suspended by two wires P and Q of equal length as shown in figure. The cross sectional areas are $1.5c{m^2}$and $1c{m^2}$. The densities of these materials are $7.8gm/cc$and $2.6gm/cc$ respectively. At what point along the rod should a weight $w$ be suspended in order to produce equal stress in strings. What is the ratio of velocities of transverse waves in these strings?

Answer 1

We know that when the rod is suspended by wires, tension is produced is both the ropes. We need to find the point of suspension of the rod so that the stress produced in both the wires is equal. For this we will need to use concepts of stress in wire and moment due to tension at a point of suspension. We are also asked to determine the ratio of velocities of transverse waves in these strings which we will do by using the relation of transverse velocity with tension and linear density.

Formulas used:
$\sigma = \dfrac{T}{A}$
where, $\sigma$ is the stress, $T$ is the tension and $A$ is the cross sectional area.
$M = Tl$
where, $M$ is the moment about a certain point, $T$ is the tension and $l$ is the perpendicular distance from the point at which the force is applied.
$v = \sqrt {\dfrac{T}{\mu }}$
where, $v$ is the velocity of the transverse wave, $T$ is the tension in the string and $\mu$ is the linear density.
$\mu = A\rho$
where $\mu$ is the linear density, $A$ is the cross sectional area and $\rho$ is the density.

Complete step by step answer:
We are asked to find the point of suspension of the rod so that the stress produced in both the wires is equal.
${\sigma _P} = {\sigma _Q}$
We know that $\sigma = \dfrac{T}{A}$.
$\dfrac{{{T_P}}}{{{A_P}}} = \dfrac{{{T_Q}}}{{{A_Q}}} \\\ \Rightarrow \dfrac{{{T_P}}}{{{T_Q}}} = \dfrac{{{A_P}}}{{{A_Q}}} \\\$
We are given that ${A_P} = 1.5c{m^2}$and ${A_Q} = 1c{m^2}$.
$\dfrac{{{T_P}}}{{{T_Q}}} = \dfrac{{1.5}}{1} \\\ \Rightarrow \dfrac{{{T_P}}}{{{T_Q}}}= \dfrac{3}{2}$
Now, we will take a moment about the point of suspension.
Let the distance of this point from the P end is $xm$. As the total length of the rod is given as $1m$, the distance of the point from the Q end will be $\left( {1 - x} \right)m$.
Applying the formula $M = Tl$, we get
${T_P} \times x = {T_Q} \times \left( {1 - x} \right) \\\ \Rightarrow \dfrac{{{T_P}}}{{{T_Q}}} = \dfrac{{\left( {1 - x} \right)}}{x} \\\$
We have determined that $\dfrac{{{T_P}}}{{{T_Q}}} = \dfrac{3}{2}$
$\Rightarrow \dfrac{3}{2} = \dfrac{{\left( {1 - x} \right)}}{x} \\\ \Rightarrow 3x = 2 - 2x \\\ \Rightarrow 5x = 2 \\\ \Rightarrow x = \dfrac{2}{5} = 0.4m \\\$
Thus the weight $w$ should be suspended at $0.4m$ distance from the P end.
Now, the velocity of the transverse wave is given by $v = \sqrt {\dfrac{T}{\mu }}$.
${v_P} = \sqrt {\dfrac{{{T_P}}}{{{\mu _P}}}}$ and ${v_Q} = \sqrt {\dfrac{{{T_Q}}}{{{\mu _Q}}}}$
$\Rightarrow \dfrac{{{v_P}}}{{{v_Q}}} = \sqrt {\dfrac{{{T_P}}}{{{T_Q}}} \times \dfrac{{{\mu _Q}}}{{{\mu _P}}}}$
We know that $\mu = A\rho$.
$\Rightarrow \dfrac{{{v_P}}}{{{v_Q}}} = \sqrt {\dfrac{{{T_P}}}{{{T_Q}}} \times \dfrac{{{A_Q}{\rho _Q}}}{{{A_P}{\rho _P}}}}$
We are given that ${A_P} = 1.5c{m^2}$, ${A_Q} = 1c{m^2}$, ${\rho _P} = 7.8gm/cc$and ${\rho _Q} = 2.6gm/cc$. And we have determined that $\dfrac{{{T_P}}}{{{T_Q}}} = \dfrac{3}{2}$.

\therefore\dfrac{{{v_P}}}{{{v_Q}}}= \dfrac{1}{{\sqrt 3 }}$$ **Thus, the ratio of velocities of transverse waves in the strings is $1:\sqrt 3 $.** **Note:** The most important thing to keep in mind while solving this question is calculating the value of linear density. This is because here, if we use the densities given in the question directly to find the velocity, we will get the wrong answer. Therefore, the densities should be multiplied by the cross section areas of the wires to find their linear velocities.