Question

A $1kg$ stone is tied to a $0.5m$ string and swung in a vertical circle. What is the tension in the string at the bottom of the loop?

Answer 1

To solve this question here we will use concept of newton's law of motion and conservation of energy, firstly, we will apply newton's law of motion to obtain the equation from where we are going to find the tension of the string and then we will apply conservation of energy to find the value of velocity for this there will be one point that we are using critical velocity and then put all the obtained and given values in the firstly obtained equation and solving we will get our required solution.

Formula used:
$K.E = \dfrac{1}{2}m{v^2}$
$P.E = mgh$
$m$ is the mass of the stone,
$v$ is the velocity.
$g$ is the acceleration due to gravity .
$h$ is the height.
${v_{{\text{critical}}}} = \sqrt {rg}$

Complete step by step solution:

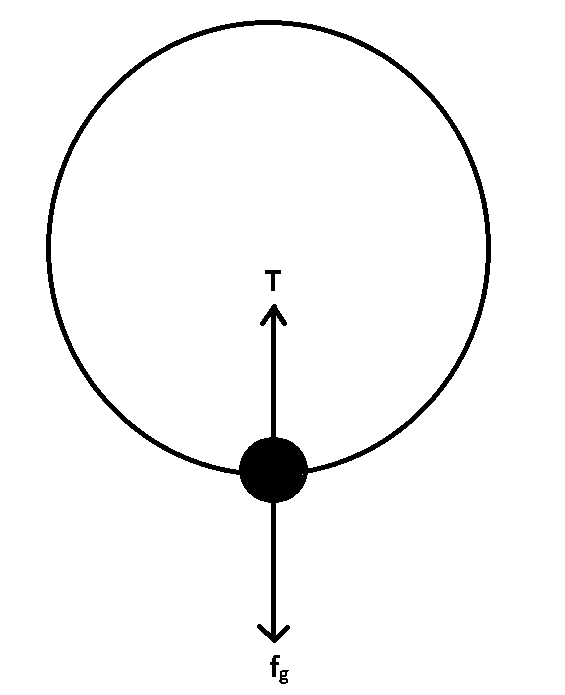
According to the question,
Mass of the stone, $m = 1kg$ ,
Length of the string is $0.5m$ and
Acceleration due to gravity,$g = 9.8m{\text{ }}{s^{ - 2}}$
From the figure we can say that,
$T - {f_g} = m{a_c}$
And we know that centripetal acceleration is given by,
${a_c} = \dfrac{{{v^2}}}{r}$
So, we can write the above equation as,
$T - {f_g} = \dfrac{{m{v^2}}}{r}$
And we know that the force by gravity is${f_g} = mg$
Therefore, we can solve the above equation and we will get,
$T - {f_g} = \dfrac{{m{v^2}}}{r}$
$\Rightarrow T = \dfrac{{m{v^2}}}{r} + mg$ -----(1)
Now, we have to calculate the velocity to get the required solution, and for that here we will use the conservation of energy.
Here we can say that at the top of the loop, the stone has both the Potential as well as kinetic energy.
We can easily say that at the bottom the stone has only kinetic energy as $h = 0$ .
As the height of the string is $h$ equal to the diameter of the circle, so we can say $h = 2r$.
So, we can write that,
$\Delta E = \Delta K.E + \Delta U$
$\dfrac{1}{2}mv_{{\text{top}}}^2 + mg(2r) = \dfrac{1}{2}mv_{{\text{bottom}}}^2$
We'll suppose that the velocity at the top of the loop is the critical velocity, or the lowest velocity required to maintain circular motion, where:
${v_{{\text{critical}}}} = \sqrt {rg}$
Putting the value in above equation,
$\dfrac{1}{2}mrg + mg(2r) = \dfrac{1}{2}mv_{{\text{bottom}}}^2$
$\dfrac{1}{2}mrg + mg(2r) = \dfrac{1}{2}mv_{{\text{bottom}}}^2 \\\ \Rightarrow v_{{\text{bottom}}}^2 = \dfrac{{2\left( {\dfrac{1}{2}mrg + 2mrg} \right)}}{m} \\\$
On further solving,
$\Rightarrow v_{{\text{bottom}}}^2 = \dfrac{{mrg + 4mrg}}{m} \\\ \Rightarrow v_{{\text{bottom}}}^2 = 5rg \\\$
Now, finally putting all these obtained and given values in equation (1)

$$T = \dfrac{{m{v^2}}}{r} + mg \\\ \Rightarrow T = \dfrac{{m \times 5rg}}{r} + mg \\\ \Rightarrow T = 5g + g \\\ \Rightarrow T = 6g \\\$$

Now putting the value of $g$ in the above equation,

$$T = 6g \\\ \Rightarrow T = 6 \times 9.8 \\\ \Rightarrow T = 58.8N \\\$$

Approximately we can say that the tension in the string at the bottom of the loop is $59N$ .

Note:
At first you will see this as a simple question but when you see that the velocity is not given there is the turning point to this question you must remember the value of critical velocity and how to apply conservation of energy. The term "conservation" refers to a situation in which nothing changes. As a result, a conserved quantity's variable in an equation remains constant across time. Its value does not change before or after a certain event.