Question

A $1kg$ block situated on a rough inclined plane is connected to a spring of spring constant $100N{{m}^{-1}}$ as shown in the figure. The block is released from rest with the spring in the unstretched position. The block moves $10cm$ along the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless. Take $g=10m{{s}^{-2}}$.

Answer 1

The reaction force due to the inclined plane on the block is calculated. Frictional force is found out using this reaction force. Net force on the block down the incline is determined by taking into consideration this frictional force also. Finally, work done in the whole process is equated to the potential energy of the stretched spring.

Complete answer:
As shown in the figure, let us consider a block of mass $1kg$ connected to a spring of spring constant $100N{{m}^{-1}}$. The block is situated on a rough inclined plane. It can be understood from the figure that the angle of inclination of the inclined plane is equal to $37{}^\circ$. It is said that the block is released from rest with the spring in the unstretched position. Once the block is released, the block moves $10cm$ along the incline before coming to rest. We are required to find the coefficient of friction between the block and the inclined plane. Firstly, let us name the mass of the block, spring constant of the spring, displacement of the block and angle of inclination of the plane as $m,K,x$ and $\theta$, respectively. Clearly,
$m=1kg;K=100N{{m}^{-1}};\theta =37{}^\circ$ and $x=10cm=0.1m$
It is obvious that the inclined plane produces a reaction force on the block when the block starts moving. Let this reactional force be denoted as $R$. It is given by
$R=mg\cos \theta$
where
$R$ is the reaction force
$m$ is the mass of the block
$g$ is the acceleration due to gravity
$mg$ is the weight of the block due to gravitational force
$\theta$ is the angle of inclination of the plane from the ground
$mg\cos \theta$ is the component of weight acting along the reaction force.
Let this be equation 1.

The diagram below gives a clear picture of the same.

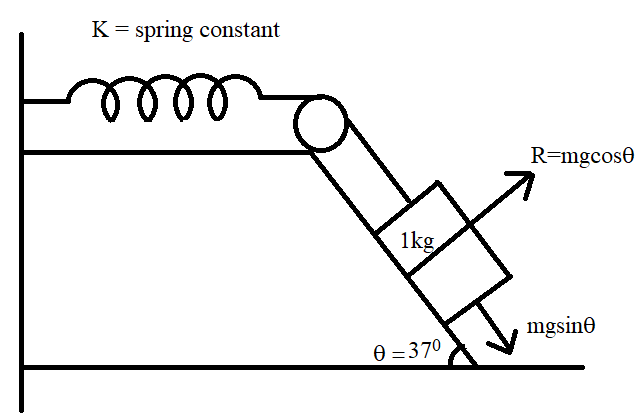
When the block starts moving, frictional force too comes into action. Let this frictional force be denoted as $F$. It is given by
$F=\mu R$
where
$F$ is the frictional force on the block
$\mu$ is the coefficient of friction between the block and the inclined plane
$R$ is the reaction force acting on the block in the direction of $mg\cos \theta$
Let this be equation 2.

The block starts moving because of a force equal to $mg\sin \theta$, which is nothing but the component of weight of the block along the inclined surface. Taking into consideration all these forces on the block, the net force acting on the block when it moves over the inclined plane is given by
${{F}_{net}}=mg\sin \theta -F$
where
we have assumed that the net force on the block is ${{F}_{net}}$
$F$ is the frictional force acting on the block
Substituting the value of frictional force from equation 2 in the above expression, we have
${{F}_{net}}=mg\sin \theta -F=mg\sin \theta -\mu R$
Substituting the value of $R$ from equation 1 in the above expression, we have
${{F}_{net}}=mg\sin \theta -\mu mg\cos \theta$
Let this be equation 3.

We are required to calculate the value of $\mu$ in the above expression. Unfortunately, we cannot determine this value of coefficient of friction from the above expression directly because we don’t know the value of force exerted on the block.
To proceed, let us calculate the work done by the spring when the block is released and equate it to the potential energy of the stretched spring because both have equal values in equilibrium.
Let the work done by the spring be denoted as $W$. Work is equal to the product of force and displacement and is given by
$W={{F}_{net}}\times x$
where
$W$ is the work done by the spring
${{F}_{net}}$ is the net force on the block
$x$ is the displacement of the block
Let this be equation 4.
Potential energy of the stretched spring is given by
$P=\dfrac{1}{2}K{{x}^{2}}$
where
we have assumed that the potential energy of the stretched spring is denoted as $P$
$K$ is the spring constant of the spring
$x$ is the displacement of the spring
Let this be equation 5.

In equilibrium, equation 4 is equal to equation 5 as already mentioned. Therefore,
$W=P\Rightarrow {{F}_{net}}\times x=\dfrac{1}{2}K{{x}^{2}}\Rightarrow {{F}_{net}}=\dfrac{1}{2}Kx$
Let this be equation 6.

Now, substituting equation 3 in equation 6, we have
${{F}_{net}}=\dfrac{1}{2}Kx=mg\sin \theta -\mu mg\cos \theta$
Substituting values from the question in the above expression, we have
$\dfrac{1}{2}Kx=mg\sin \theta -\mu mg\cos \theta \Rightarrow \dfrac{1}{2}\times 100\times 0.1=1\times 10(\sin 37{}^\circ -\mu \cos 37{}^\circ )\Rightarrow 5=10(\sin 37{}^\circ )-10\mu \cos 37{}^\circ$
On simplification,
$5=10(\sin 37{}^\circ )-10\mu \cos 37{}^\circ =10\times 0.601-10\mu \times 0.798=6.01-\mu \times 7.98\Rightarrow \mu =\dfrac{6.01-5}{7.98}=0.126$
Therefore, the value of coefficient of friction $(\mu )$ is equal to $0.126$

So, the correct answer is “Option A”.

Note:
It is mentioned that the potential energy of the stretched string is equal to the work done by the spring on the block. Students should understand that this work done by the spring is nothing but the work done on the block when it moves on the inclined plane. It is equal to the product of force acting on the block and displacement caused due to this force. Since the spring is well-connected to the block, there is transfer of energy and both works can be related. Also, to be noted that the displacement in the block is equal to the displacement in the stretched spring.