Question

A $1kg$ block situated on a rough incline is connected to a spring of negligible mass having spring constant $100N{m^{ - 1}}$ as shown in figure. The block is released from rest with the spring in the un starched position. The block moves $10cm$ down the incline before coming to rest. The co-0efficient of friction between the block and the incline is____________. (Take $g = 10m{s^{ - 2}}$ and assume that the pulley is frictionless.)
A) $0.2$
B) $0.3$
C) $0.5$
D) $0.6$

Answer 1

Rembert, to solve the question in which there are different forces are acting, consider the whole system is equilibrium and equate the net force acting in the opposite direction. Do not forget the required unit conversions.

Complete step by step solution:
Let’s define all the terms given in the question itself:
Mass of the block is, $m = 1kg$
Angle of the inclined plane is, $\theta = 45^\circ$
Spring constant of the spring to which the block is connected, $K = 100N{m^{ - 1}}$
Distance of the movement of block down the inclined plane before coming to rest:
$x = 10cm$ $= 10 \times {10^{ - 2}}m$
Value of gravitational constant, $g = 10m{s^{ - 2}}$

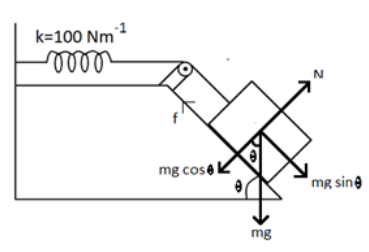
From the figure,
We know the value of the frictional force is given by the equation:
$f = \mu N$
Where, $\mu$ is the coefficient of friction between the block and the incline plane.
$N$ is the normal force acting on the block on the inclined plane.
From the diagram, we can understand that the value of $N$ is given by,
$N = mg\cos \theta$
So, frictional force, $f = \mu mg\cos \theta$
When we consider the net force acting down through the incline (from the diagram)
$= mg\sin \theta - f$
$= mg\sin \theta - \mu mg\cos \theta$
$= mg(\sin \theta - \mu \cos \theta )$
For the equilibrium condition, it should be follow the following condition:
That is, Work done = Potential energy of stretched spring…………….. (1)
The work done in terms of the net force acting and the distance moved is given by,
Work done= $$$$ $net{\text{ }}force{\text{ }}acting \times {\text{ }}distance{\text{ }}moved$
$W = mg(\sin \theta - \mu \cos \theta ) \times x$
Stretched spring’s potential energy of the is given by,
$P.E. = \dfrac{1}{2}K{x^2}$
Applying these values to the equation (1)
$\Rightarrow mg(\sin \theta - \mu \cos \theta ) \times x = \dfrac{1}{2}K{x^2}$
$\Rightarrow 2mg(\sin \theta - \mu \cos \theta ) = Kx$
Applying all the known values of all the terms in this equation, we get,
$2 \times 1 \times 10 \times (\sin 45 - \mu \cos 45) = 100 \times 10 \times {10^{ - 2}}$ $\Rightarrow sin45 - \mu \cos 45 = \dfrac{1}{2}$
$\Rightarrow \dfrac{1}{{\sqrt 2 }} - \dfrac{\mu }{{\sqrt 2 }} = \dfrac{1}{2}$
$\Rightarrow 1 - \mu = \dfrac{{\sqrt 2 }}{2}$
$\Rightarrow \mu = \dfrac{{\sqrt 2 - 1}}{{\sqrt 2 }}$
$\therefore \mu = 0.3$
That is, the co-0efficient of friction in-between the block and the incline is given by , $\mu = 0.3$
Final answers option (B), $0.3$.

Note: There are essentially two kinds of coefficients; static and kinetic. The static coefficient of friction is the coefficient of friction that applies to objects that are motionless. The kinetic or sliding coefficient of friction is the coefficient of friction that applies to objects that are in motion.