Question

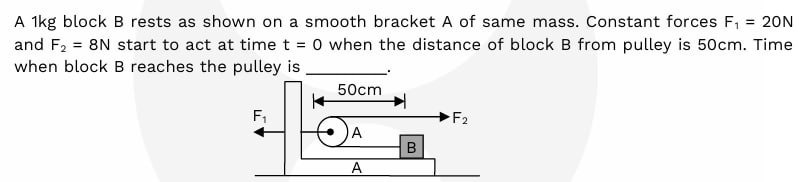
A 1kg block B rests as shown on a smooth bracket A of same mass. Constant forces F₁ = 20N and F₂ = 8N start to act at time t = 0 when the distance of block B from pulley is 50cm. Time when block B reaches the pulley is ___________________.

Answer 1

0.5 s

Answer 2

To determine the time when block B reaches the pulley, we need to analyze the forces acting on block B and bracket A.

1. Identify the forces: The force $F_2 = 8$ N applied to the string creates a tension $T = 8$ N in the string.

2. Forces on block B: The tension $T$ pulls block B to the left. Applying Newton's second law:

   $m_B a_B = T \implies 1 \cdot a_B = 8 \implies a_B = 8 \, \text{m/s}^2$ (to the left).

3. Forces on bracket A: Two horizontal forces act on bracket A:

   • $F_1 = 20$ N acts to the left.
   • The string passing over the pulley exerts a force on the pulley (which is part of A). This force is $2T$ and acts in the direction opposite to the applied force $F_2$ relative to the pulley's motion. More simply, the force exerted by the string on the bracket A is $2T = 2 \times 8 = 16$ N to the right.

   Therefore, the net force on A is $F_{\text{net}, A} = F_1 \text{ (left)} - 2T \text{ (right)} = 20 - 16 = 4$ N (to the left). Applying Newton's second law:

   $m_A a_A = 4 \implies 1 \cdot a_A = 4 \implies a_A = 4 \, \text{m/s}^2$ (to the left).

4. Relative acceleration: Calculate the relative acceleration of block B with respect to bracket A. Let the left direction be positive.

   $a_{B/A} = a_B - a_A = 8 \, \text{m/s}^2 - 4 \, \text{m/s}^2 = 4 \, \text{m/s}^2$ (to the left).

   Since $a_{B/A}$ is to the left, block B moves towards the pulley.

5. Kinematics: The initial distance of block B from the pulley is $50 \, \text{cm} = 0.5 \, \text{m}$. Using the kinematic equation for constant acceleration: $s = v_0 t + \frac{1}{2} a t^2$. Since the blocks start from rest, $v_0 = 0$.

   $0.5 = 0 + \frac{1}{2} (4) t^2$ $0.5 = 2 t^2$ $t^2 = 0.25$ $t = \sqrt{0.25} = 0.5 \, \text{s}$.

Therefore, the time when block B reaches the pulley is 0.5 s.