Question

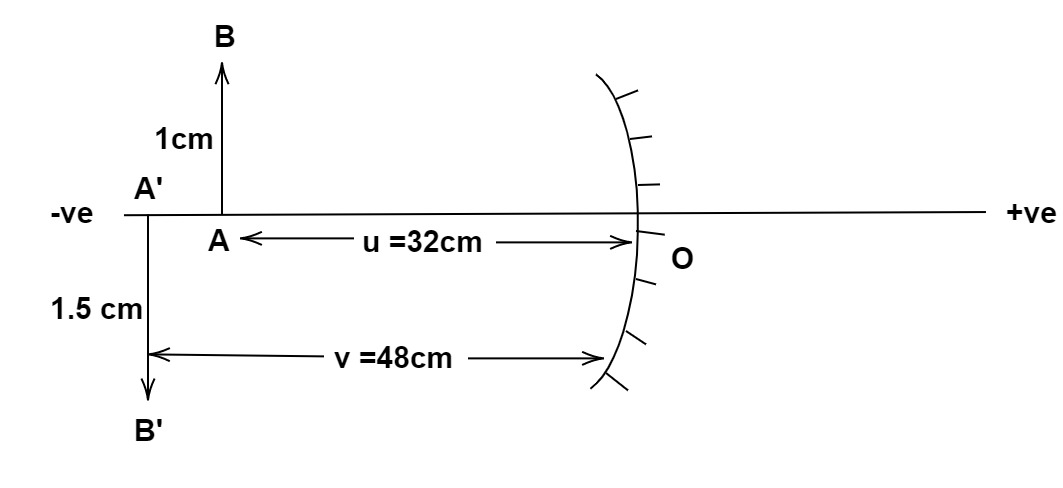
A $1cm$ high object is placed at a distance of $32cm$ from a concave mirror. The image is real, inverted and $1.5cm$ in size. Calculate the focal length of the mirror and the position of the image.

Answer 1

Here we know the height of the object, height of the image and distance of the object is known to us. Now using the magnification formula of the concave mirror we can find the relation between the heights of the object, height of the image, image distance and the object distance. From that we can find the value of the image distance from the concave mirror. Now using the mirror formula we can calculate the focal length of the mirror.

Complete step by step answer:
As per the problem we have a $1cm$ high object is placed at a distance of $32cm$ from a concave mirror. The image is real, inverted and $1.5cm$ in size.
Hence we can write the given value as:
Distance of the object placed from a concave mirror, $u = - 30cm$
Height of the object, ${h_O} = 1cm$
Height of the image, ${h_i} = - 1.5cm$
Now we know the magnification formula of the concave mirror as,
$m = \dfrac{{{h_i}}}{{{h_O}}} = \dfrac{{ - v}}{u}$
Where,
The distance of the image from a concave mirror, $v$.
Now putting the give values in the above equation we will get,
$\dfrac{1}{{ - 1.5}} = \dfrac{{ - v}}{{ - 30}}$
$\Rightarrow v = - 48cm$
Hence the distance of the image is $48cm$ from the pole and on the same side of the object.

Now using mirror formula we will get,
$\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$
Now putting the value we will get,
$\dfrac{1}{f} = \dfrac{1}{{ - 32}} + \dfrac{1}{{ - 48}}$
On solving further we will get the focal length of the concave mirror is,
$f = - 19.2cm$

Note:
Remember that concave mirrors always produce a real and virtual, erect and inverted, diminished, small size and magnified image, which depends upon the position of the object on the principle axis. Also note that in a concave mirror due to its nature of the inner reflecting surface the light rays incident on it tend to converge as the light falls on its surface.