Question
Question: A \( 16cm \) long pencil is placed as shown in figure. The central point C is \( 45cm \) away from a...
A 16cm long pencil is placed as shown in figure. The central point C is 45cm away from a 20cm focal length lens and 15cm above the optic axis. Find the length of the image.
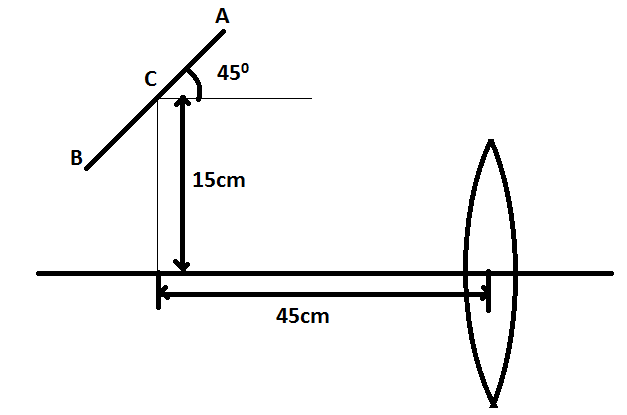
Solution
Hint : Here we are asked to find the length of the image of the pencil A′B′ . For this, we will first find the coordinates of all the three given points for its image. We will use the lens formula for finding these coordinates.
Complete Step By Step Answer:
As we are given the position of the midpoint of the pencil, we will first find the coordinates for the image of this midpoint C′ .
For point C, the object distance u=−45cm .
We know that the lens formula is: v1−u1=f1 , where, v is the image distance, u is the object distance and f is the focal length of the lens.
v1−u1=f1 ⇒v1=f1+u1=201+−451=1809−4=1805=361 ⇒v=36cm
We know that height of the image is given by: h′=uv×h , where, h′ is the height of the image, v is the image distance, u is the object distance and h is the height of the object.
We are given h=15cm for C.
⇒h′=−4536×15=−12cm
Therefore, the coordinates of C′ are (36,−12) .
Now, we will do a similar process for point B.
For B, u=−(45+8cos45)=−50.66cm
⇒v1=f1+u1=201+−50.661=331 ⇒v=33cm
The height of the point B′ will be
h′=−50.6633×(15−42)=−6.1cm
Therefore, the coordinates of B′ are (33,−6.1) .
For point A, u=−(45−8cos45)=−39.34cm
⇒v1=f1+u1=201+−39.341=40.71 ⇒v=40.7cm
The height of the point A′ will be
h′=−39.3433×(15+42)=−21.4cm
Therefore, the coordinates of A′ are (40.7,−21.4) .
Thus, the length of image of the pencil A′B′=(40.7−33)2+(−21.4−(−6.1))2=7.72+3.12=17.1cm .
Note :
In this question, we have used the concept of finding the distance between two points for determining the length of the image. Let us consider that we are given two points (a,b) and (c,d) . Then, the distance between these two points is given by (a−c)2+(b−d)2 .
