Question

Tangents are drawn at the point of intersections of the circles $x^2 + y^2 = 1$ and $x^2 + y^2 - (\lambda + 6)x + (8 - 2\lambda)y - 3 = 0$. $\lambda$ being the variable. Then the locus of the point of intersection of these tangents is :

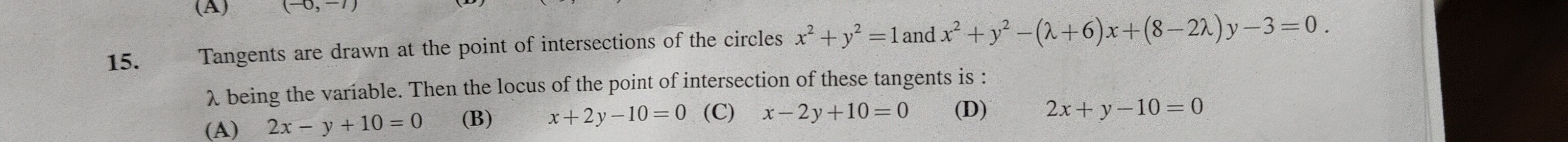
• A. 2x - y + 10 = 0
• B. x + 2y - 10 = 0
• C. x - 2y + 10 = 0
• D. 2x + y - 10 = 0

Answer 1

Answer: (A)

2x - y + 10 = 0

Answer 2

Let the two circles be $S_1 = x^2 + y^2 - 1 = 0$ and $S_2 = x^2 + y^2 - (\lambda + 6)x + (8 - 2\lambda)y - 3 = 0$. The radical axis, which is the line passing through the points of intersection of the two circles, is given by $S_1 - S_2 = 0$.

$S_1 - S_2 = (x^2 + y^2 - 1) - (x^2 + y^2 - (\lambda + 6)x + (8 - 2\lambda)y - 3) = 0$ $-1 + (\lambda + 6)x - (8 - 2\lambda)y + 3 = 0$ $(\lambda + 6)x + (2\lambda - 8)y + 2 = 0$

Let $P(x_0, y_0)$ be the point of intersection of the tangents drawn to the circle $S_1: x^2 + y^2 = 1$ at its points of intersection with $S_2$. In this case, the radical axis $(\lambda + 6)x + (2\lambda - 8)y + 2 = 0$ is the chord of contact of the tangents from $P(x_0, y_0)$ to the circle $S_1$.

The equation of the chord of contact of $P(x_0, y_0)$ with respect to $S_1: x^2 + y^2 - 1 = 0$ is given by: $xx_0 + yy_0 - 1 = 0$

This chord of contact must be identical to the radical axis. Therefore, the coefficients must be proportional: $x_0 = k(\lambda + 6)$ (1) $y_0 = k(2\lambda - 8)$ (2) $-1 = 2k$ (3)

From equation (3), we find $k = -1/2$.

Substitute $k = -1/2$ into equations (1) and (2): $x_0 = -\frac{1}{2}(\lambda + 6)$ $y_0 = -\frac{1}{2}(2\lambda - 8) = -(\lambda - 4) = 4 - \lambda$

Now, we need to eliminate $\lambda$ to find the locus of $(x_0, y_0)$. From the equation for $x_0$: $2x_0 = -(\lambda + 6)$ $2x_0 = -\lambda - 6$ $\lambda = -2x_0 - 6$

Substitute this expression for $\lambda$ into the equation for $y_0$: $y_0 = 4 - (-2x_0 - 6)$ $y_0 = 4 + 2x_0 + 6$ $y_0 = 2x_0 + 10$

Thus, the locus of $(x_0, y_0)$ is $y = 2x + 10$. Rewriting this equation, we get: $2x - y + 10 = 0$