Question

$A(1,3)$ and $C(5,1)$ are two opposite vertices of a rectangle. If the slope of the line on which other two vertices $B$ and $D$ lie is $2$, then equation of $BD$, is
A) $2x - y = 4$
B) $2x - y = 1$
C) $2x + y = 4$
D) $2x + y = 1$

Answer 1

Use the property of the diagonals of the rectangle that the intersection point of the diagonal is the midpoint of each diagonal. Find the equation of line by using the point-slope formula.

Complete step-by-step answer:
First, we draw the rectangle with the given information.

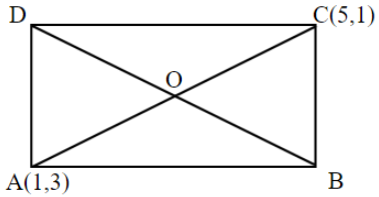
We are given that $A(1,3)$ and $C(5,1)$ are two opposite vertices of a rectangle.
Let the diagonal intersect each other at the point O.
We are also given that If the slope of the line on which other two vertices $B$ and $D$ lie is $2$.
It means if we evaluate any point on this line then we can apply the point-slope form to find the equation of line BD.
We know that the intersection point of the diagonal is the midpoint of each diagonal.
Therefore, O is the midpoint of BD and AC.
The midpoint coordinate for the points $(a,b)$ and $(c,d)$ is $\left( {\dfrac{{a + b}}{2},\dfrac{{c + d}}{2}} \right)$
Evaluate the coordinates of O with the help of $A(1,3)$and $C(5,1)$.
$O\left( {\dfrac{{1 + 5}}{2},\dfrac{{3 + 1}}{2}} \right) \\\ \Rightarrow O(3,2) \\\$
Now the point O also lies on the line BD.
We know that equation of line passing through a point $({x_1},{y_1})$ and slope $m$ is $y - {y_1} = m(x - {x_1})$
We are given the slope of the line BD is $2$, therefore $m = 2$ and a point $O(3,2)$ lies on the line BD, therefore, $({x_1},{y_1}) = (3,2)$
Substitute all the values in the given formula of the equation of line.
$y - 2 = 2(x - 3) \\\ \Rightarrow y - 2 = 2x - 6 \\\ \Rightarrow 2x - y = 4 \\\$
Therefore, equation of $BD$ is $2x - y = 4$
Hence, option (A) is correct.

Note: Since the diagonals of the rectangle are perpendicular to each other, therefore, the products of their slope are $- 1$. In these types of questions where slope is given try to find a point which lies on that line.