Question
Question: $A = \{1,2,3,4,5,6,7\}$ $B = \{3,5,6,9\}$ $S = \{C: C \subset A \text{ and } C \cap B \neq \phi\}$...
A={1,2,3,4,5,6,7} B={3,5,6,9} S={C:C⊂A and C∩B=ϕ}
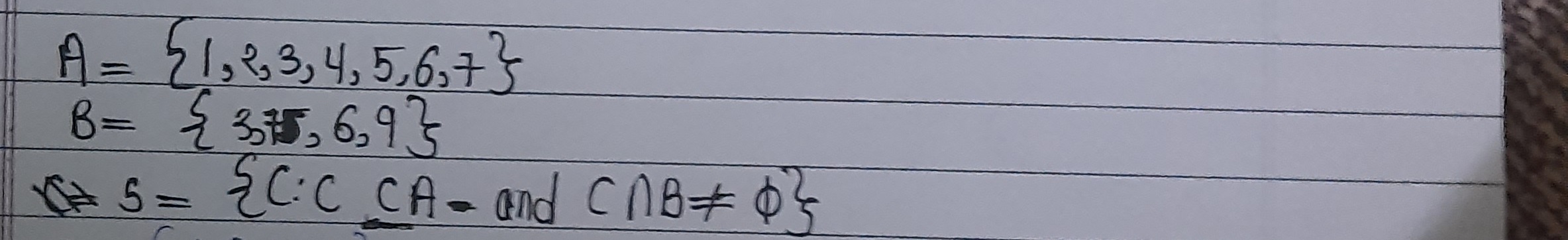
112
Solution
Let A={1,2,3,4,5,6,7} and B={3,5,6,9}. We are looking for the number of subsets C of A such that C∩B=ϕ. The elements common to A and B are A∩B={3,5,6}. The condition C∩B=ϕ means that the subset C must contain at least one element from {3,5,6}.
The total number of subsets of A is 2∣A∣=27=128.
To find the number of subsets C with C∩B=ϕ, we can subtract the number of subsets C with C∩B=ϕ from the total number of subsets of A. The condition C∩B=ϕ means that C contains no elements from B. Since C must be a subset of A, this implies C contains no elements from A∩B. Thus, C must be a subset of A∖(A∩B). A∖(A∩B)={1,2,3,4,5,6,7}∖{3,5,6}={1,2,4,7}. The number of subsets of {1,2,4,7} is 2∣{1,2,4,7}∣=24=16. These are the subsets C for which C∩B=ϕ.
The number of subsets C of A such that C∩B=ϕ is: (Total number of subsets of A) - (Number of subsets C of A such that C∩B=ϕ) =27−24=128−16=112.
