Question

Calculate the value of Activation energy at temperature of 300 K if the expression of rate constant as a function of temperature is given as $K = 30e^{\frac{-40}{300}}e^{\frac{T}{2}}$.

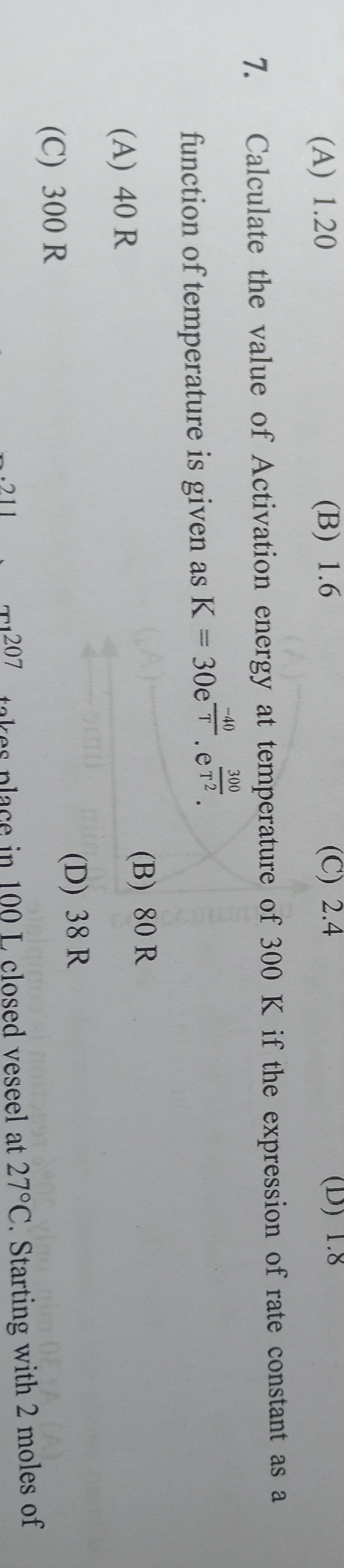
• A. 40 R
• B. 80 R
• C. 300 R
• D. 38 R

Answer 1

Answer: (A)

40 R

Answer 2

The rate constant as a function of temperature is given by $K = 30e^{\frac{-40}{300}}e^{\frac{T}{2}}$. We are asked to calculate the activation energy at $T = 300 \, \text{K}$.

Given the options and the structure of the exponent, it is highly probable that the intended activation energy is 40R. This would be the case if the rate constant was given by $K = A e^{-\frac{40R}{RT}}$.

Assume the rate constant expression was intended to be of the Arrhenius form $K = A e^{-\frac{E_a}{RT}}$, and based on the structure of the given expression and options, the activation energy is intended to be 40R. If $E_a = 40R$, then the exponent is $-\frac{40R}{RT} = -\frac{40}{T}$. This resembles the term $\frac{-40}{300}$ in the given expression.

Therefore, the activation energy is 40 R.