Question
Question: A \( 12\;cm \) wire is given a shape of a right angled triangle \( \;ABC \) having sides \( 3\;cm \)...
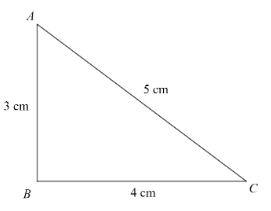
A 12cm wire is given a shape of a right angled triangle ABC having sides 3cm , 4cm , and 5cm as shown in the figure. The resistance between two ends (AB,BC,CA) of the respective sides are measured one by one by a multimeter. The resistances will be in the ratio?
(A) 3:4:5
(B) 9:16:25
(C) 27:32:35
(D) 21:24:25
Solution
To find the ratio of resistances between two ends, we need to rearrange the connection as per the considered ends, and find the equivalent resistances separately and then find the ratio of all resistances.
Complete answer:
From the given data,
Length of the component AB , l1=3cm
Length of the component BC , l2=4cm
Length of the component AC , l3=5cm
Now, we know that the resistance can be calculated as,
R=Aρl
Where ρ is the resistivity of the wire, l is the length of the wire, A is the area of the cross section of the wire.
Now, for all three resistances, the resistance is calculated as
R1=A1ρ1l1
R2=A2ρ2l2
R3=A3ρ3l3
But here as per the given conditions, a single uniform wire is bent to make the triangle.
Hence, the resistivity of all three components and the area of the cross section of all three components are the same.
∴A1ρ1=A2ρ2=A3ρ3
Suppose all the ratios as a single variable
∴A1ρ1=A2ρ2=A3ρ3=a(suppose)
Now, the values of all three resistances by substituting the given values of lengths is
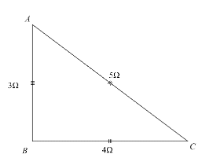
R1=3aΩ , R2=4aΩ , R3=5aΩ
Now, for simplicity of calculation we will not consider the variable
R1=3Ω , R2=4Ω , R3=5Ω
Hence, the figure can be shown as
Now, we will consider the individual components of the connection
Resistance across the ends A and B
For the considered ends, the circuit can be explained as R2 and R3 connected in series connection and whole connected in parallel connection with R1 as shown below,
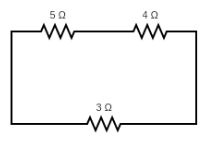
Equivalent resistance for the resistors R2 and R3 is
R′=R2+R3
Substituting the values,
R′=4Ω+5Ω
∴R′=9Ω
This equivalent resistance and R1 are connected in parallel. Hence, the equivalent resistance is
Req=R1+R′R1R′
Substituting the values,
∴Req1=3+93×9
∴Req1=1227Ω …… (1)
Resistance across the ends B and C
For the considered ends, the circuit can be explained as R1 and R3 connected in series connection and whole connected in parallel connection with R2 as shown below,
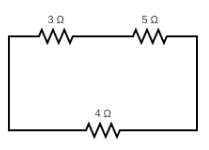
Equivalent resistance for the resistors R1 and R3 is
R′=R1+R3
Substituting the values,
R′=3Ω+5Ω
∴R′=8Ω
This equivalent resistance and R2 are connected in parallel. Hence, the equivalent resistance is
Req=R2+R′R2R′
Substituting the values,
∴Req2=4+84×8
∴Req2=1232Ω …… (2)
Resistance across the ends C and A
For the considered ends, the circuit can be explained as R1 and R2 connected in series connection and whole connected in parallel connection with R3 as shown below,
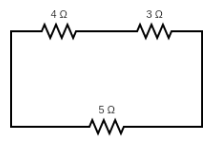
Equivalent resistance for the resistors R1 and R2 is
R′=R1+R2
Substituting the values,
R′=3Ω+4Ω
∴R′=7Ω
This equivalent resistance and R3 are connected in parallel. Hence, the equivalent resistance is
Req=R3+R′R3R′
Substituting the values,
∴Req3=5+75×7
∴Req3=1235Ω …… (3)
Taking the ratio of all the cases,
Req1:Req2:Req3=1227:1232:1235
∴Req1:Req2:Req3=27:32:35
Hence, the correct answer is Option (C) .
Note:
The value of the resistances are directly taken equal to the length of the resistances for simplicity, as they are considered in a ratio and the common factor will be canceled eventually. However, this can only be done, if all the three wires are given to be of the same material and same area.
