Solveeit Logo
Login

Question

Question: A 12.5eV electron beam is used to excite a gaseous hydrogen atom at room temperature. Determine the ...

A 12.5eV electron beam is used to excite a gaseous hydrogen atom at room temperature. Determine the wavelengths and the corresponding series of the lines emitted.

Explanation

Solution

Firstly, you could go for finding the energy after excitation of the hydrogen and thus determine its final excited state. After that you could find all possible transitions. Then you could find the energy difference of these levels and also the wavelength of the radiation emitted.
Formula used:
Energy of nth energy level,
En=−13.6eVn2{{E}_{n}}=\dfrac{-13.6eV}{{{n}^{2}}}
Wavelength,
λ=hcE\lambda =\dfrac{hc}{E}

Complete answer:
We are given that the gaseous hydrogen atom is excited using a 12.5eV electron beam at room temperature. Then, its energy after excitation would be,
E=−13.6eV+12.5eV=−1.1eVE=-13.6eV+12.5eV=-1.1eV
We know that energy of the nth energy level is given by,
En=−13.6eVn2{{E}_{n}}=\dfrac{-13.6eV}{{{n}^{2}}}
⇒−13.6n2=−1.1eV\Rightarrow \dfrac{-13.6}{{{n}^{2}}}=-1.1eV
⇒n=3.51⟨4\Rightarrow n=3.51\langle 4
∴n≈3\therefore n\approx 3
So we found the final excited state to be n = 3.
So the possible transitions would be,
(a) n=3→n=2n=3\to n=2
(b) n=3→n=1n=3\to n=1
(c) n=2→n=1n=2\to n=1

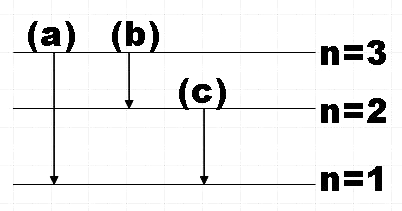
For the transition fromn=3→n=2n=3\to n=2,
ΔE=E3−E2=−13.632−(−13.622)\Delta E={{E}_{3}}-{{E}_{2}}=\dfrac{-13.6}{{{3}^{2}}}-\left( \dfrac{-13.6}{{{2}^{2}}} \right)
⇒ΔE=−1.51+3.4\Rightarrow \Delta E=-1.51+3.4
∴ΔE=1.89eV\therefore \Delta E=1.89eV
Corresponding wavelength,
λ=hcE\lambda =\dfrac{hc}{E}
⇒λ=6.6×10−34×3×1081.89×1.6×10−19\Rightarrow \lambda =\dfrac{6.6\times {{10}^{-34}}\times 3\times {{10}^{8}}}{1.89\times 1.6\times {{10}^{-19}}}
∴λ=6547.6A∘\therefore \lambda =6547.6A{}^\circ
So we found that this belongs to the Balmer series.
For the transition fromn=3→n=1n=3\to n=1,
ΔE=E3−E1=−13.632−(−13.612)\Delta E={{E}_{3}}-{{E}_{1}}=\dfrac{-13.6}{{{3}^{2}}}-\left( \dfrac{-13.6}{{{1}^{2}}} \right)
⇒ΔE=−1.51+13.6\Rightarrow \Delta E=-1.51+13.6
∴ΔE=12.09eV\therefore \Delta E=12.09eV
Corresponding wavelength,
λ=hcE\lambda =\dfrac{hc}{E}
⇒λ=6.6×10−34×3×10812.09×1.6×10−19\Rightarrow \lambda =\dfrac{6.6\times {{10}^{-34}}\times 3\times {{10}^{8}}}{12.09\times 1.6\times {{10}^{-19}}}
∴λ=1023A∘\therefore \lambda =1023A{}^\circ
So, we found that this belongs to the Lyman series.
For the transition fromn=2→n=1n=2\to n=1,
ΔE=E3−E1=−13.622−(−13.612)\Delta E={{E}_{3}}-{{E}_{1}}=\dfrac{-13.6}{{{2}^{2}}}-\left( \dfrac{-13.6}{{{1}^{2}}} \right)
⇒ΔE=−3.4+13.6\Rightarrow \Delta E=-3.4+13.6
∴ΔE=10.2eV\therefore \Delta E=10.2eV
Corresponding wavelength,
λ=hcE\lambda =\dfrac{hc}{E}
⇒λ=6.6×10−34×3×10810.2×1.6×10−19\Rightarrow \lambda =\dfrac{6.6\times {{10}^{-34}}\times 3\times {{10}^{8}}}{10.2\times 1.6\times {{10}^{-19}}}
∴λ=1213A∘\therefore \lambda =1213A{}^\circ
We found that this belongs to the Lyman series.

Note:
We should understand that the Hydrogen’s emission spectrum is basically divided into a number of spectral series. Also we know that they are observed as the result of electron transitions in various energy levels. We could also classify these series as Lyman series, Balmer series, Paschen series, Brackett series and Pfund series.