Question

A 10V Battery with internal resistance 1Ω and a 15V battery with internal resistance 0.6Ω are connected in parallel to a voltmeter. What is the closest reading in the voltmeter from the given options?

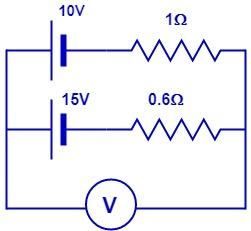
(A) 11.9V
(B) 13.1V
(C) 24.5V
(D) 12.5V

Answer 1

Use the Kirchhoff’s voltage law in the circuit to get the required voltage of the voltmeter.
Kirchhoff’s Voltage Law (KVL) is Kirchhoff’s second law that deals with the conservation of energy around a closed circuit path.
This voltage law states that for a closed loop series path the algebraic sum of all the voltages around any closed loop in a circuit is equal to zero. This is because a circuit loop is a closed conducting path so no energy is lost.
In other words the algebraic sum of all the potential differences around the loop must be equal to zero as:
$\sum{V}=0$

Complete step by step answer:

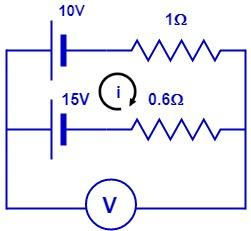
Using Kirchhoff’s Voltage Law in the given circuit we get:
$\begin{aligned} &\Rightarrow 15-10-1\cdot i-0.6\cdot i=0 \\\ &\Rightarrow 5-1.6\cdot i=0 \\\ &\Rightarrow 1.6\cdot i=5 \\\ &\Rightarrow i=\dfrac{5}{1.6} \\\ &\Rightarrow i=3.125A \\\ \end{aligned}$
Here the voltmeter reading is given by the potential difference across the lower circuit with 15V battery. So again applying the Kirchhoff’s Voltage Law here we get:
$\begin{aligned} &\Rightarrow \Delta V=15-0.6i \\\ &\Rightarrow15-0.6\times 3.125 \\\ &\Rightarrow15-1.875 \\\ &\Rightarrow \Delta V=13.125V \\\ \end{aligned}$
Hence the closest value of the voltmeter reading in the options is (B) 13.1V.

Note:
While applying the KVL, always use the correct sign of conventions for the voltage of each resistor to avoid mistakes. The term “algebraic sum” in the voltage law means to take into account the polarities and signs of the sources and voltage drops around the loop.